Les technologies quantiques sont largement considérées comme le prochain sommet à atteindre en informatique, mais on peut emprunter plusieurs voies pour y parvenir. Dans le monde entier, des chercheurs étudient différentes manières de mettre au point des ordinateurs quantiques robustes et adaptables, en exploitant tout ce qui est possible, des lasers optiques à l’intrication quantique.

Une voie a longtemps été considérée comme trop théorique pour pouvoir être mise à l’épreuve et appliquée en pratique. Mais grâce à un article publié par une équipe travaillant au Canada, elle pourrait ne plus rester longtemps hors des sentiers battus.

L’article intitulé Experimental Identification of Non-Abelian Topological Orders on a Quantum Simulator (Identification expérimentale d’ordres topologiques non abéliens dans un simulateur quantique), publié en février dans Physical Review Letters, rapporte que des théoriciens et des expérimentateurs ont trouvé un intermédiaire entre la théorie exotique et l’expérience réalisable.

Les chercheurs ont montré comment un ordinateur possédant un circuit de calcul quantique peut servir à simuler l’informatique quantique topologique.

Ils ont ainsi complété la première étape d’un programme de recherche qui, espèrent-ils, donnera un ordinateur quantique insensible aux défaillances, et dont la puissance et la stabilité ne viendront pas des pièces infinitésimales qui composent l’ordinateur, mais du comportement de l’ensemble du système.

Yidun Wan, ancien postdoctorant à l’Institut Périmètre[/caption]

« Je crois qu’il s’agit d’une nouvelle avenue pour l’informatique quantique », déclare Yidun Wan, qui a lancé ce projet de recherche avec son collègue Ling-Yan Hung, alors que les deux étaient postdoctorants à l’Institut Périmètre en 2016. Ils sont maintenant professeurs à l’Université Fudan de Shanghai.

« Les gens pensaient à des circuits de calcul quantique ou à l’informatique quantique topologique, poursuit-il. Cette avenue se situe un peu entre les deux. Nous exploitons les avantages des deux méthodes. » [traduction]

En théorie, l’informatique quantique topologique (IQT) est extrêmement prometteuse. La matière topologique tire son nom du fait que son comportement est dicté par sa forme : si vous prenez deux morceaux d’un matériau topologique, et que vous donnez à l’un la forme d’une sphère et à l’autre la forme d’un tore (comme un beigne avec un trou au milieu), le traitement de l’information à l’aide de ces systèmes à l’origine identiques donnera deux résultats totalement différents.

Comme le calcul est dicté par l’entité dans son ensemble, les systèmes topologiques sont censés être très robustes. Ils sont en cela bien différents des autres formes de systèmes d’informatique quantique, qui reposent sur la manipulation de bits quantiques (ou qubits) individuels et sont de ce fait extrêmement sensibles aux perturbations extérieures, ce qui les rend vulnérables à des « erreurs locales ».

En pratique toutefois, le calcul quantique topologique n’est pas près de se concrétiser, car les scientifiques n’ont pas encore établi quel système physique permettrait de le réaliser.

Par conséquent, au lieu d’attendre le système physique parfait permettant de faire une démonstration expérimentale d’IQT, M. Wan a proposé d’utiliser une technologie existante — un ordinateur possédant un circuit de calcul quantique — pour simuler un ordinateur quantique topologique. Les chercheurs ont fait une démonstration de ce compromis à l’Institut d’informatique quantique de l’Université de Waterloo, et les résultats ont été qualifiés de point tournant. L’un des pairs examinateurs de l’article a décrit ces résultats comme « une étape-clé de la réalisation physique du calcul quantique topologique » [traduction].

Cette voie hybride ne fournit pas toute la puissance d’un véritable calcul quantique topologique, mais elle donne un bon aperçu de ce qui serait possible.

Les ingrédients de l’informatique quantique

L’unité fondamentale de l’informatique classique est le bit. Cette unité peut prendre l’une des valeurs 1 ou 0, ce qui fonctionne bien mais limite la quantité de données que l’on peut traiter.

L’analogue quantique d’un ordinateur de bureau est l’ordinateur possédant un circuit de calcul quantique. Dans ce cas-ci, l’unité fondamentale d’information est le qubit (pour « bit quantique »), généralement incarné par un ion ou un électron. À cause de sa ressemblance avec l’ordinateur classique, l’ordinateur possédant un circuit de calcul quantique constitue la porte d’entrée traditionnelle pour les gens qui abordent le domaine. Le principal inconvénient de cette méthode est qu’elle est sensible aux erreurs locales — dues à des champs magnétiques et à d’autres perturbations extérieures. Pour contrer cela, le système comporte des dispositifs de correction des erreurs quantiques. Les calculs sont alors plus exacts, mais la grande majorité des qubits sert à corriger les erreurs plutôt qu’à effectuer les calculs eux-mêmes.

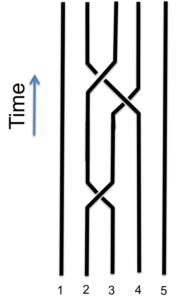
Exemple de la manière dont les chemins des anyons de Fibonacci peuvent se croiser dans le temps
Légende : Time = Temps[/caption]

La démarche de l’IQT est totalement différente. Au lieu d’utiliser des particules spécifiques comme qubits, l’IQT fait appel à des anyons, quasiparticules exotiques qui ne sont ni des fermions (électrons, protons, etc.), ni des bosons (photons, gluons, etc.). Ces anyons sont déplacés d’une manière particulière, de telle sorte que les chemins qu’ils parcourent se croisent à mesure que le temps s’écoule [voir la figure à droite].

Comme lorsque l’on tresse des cheveux, l’IQT ne fonctionne que si les anyons font un croisement à la fois, et seulement dans certaines directions. (Si deux mêmes brins se croisent dans un sens puis dans l’autre, sans boucle, les deux peuvent être simplement écartés l’un de l’autre.) Chaque croisement de chemins d’anyons devient une porte où un calcul est effectué. Comme le calcul résulte du comportement du système, il est largement imperméable aux erreurs locales. Il est de fait insensible aux défaillances.

Il existe un certain nombre de types différents de quasiparticules. Lorsque l’IQT a été proposée pour la première fois, en 1997, l’idée reposait sur un type spécifique de quasiparticules appelées anyons non abéliens (une modification de l’ordre des mouvements des anyons a pour effet de modifier leur parcours final). Les anyons de Fibonacci ont un intérêt particulier. Le nom bien connu de Fibonacci ne figure pas ici par hasard. À mesure que les anyons interagissent et s’unissent, les dimensions du système augmentent selon la suite de Fibonacci.

Il faut d’abord comprendre que la théorie des anyons est définie dans ce que l’on appelle un espace de Hilbert, espace d’un nombre quelconque de dimensions que l’on rencontre souvent en physique et en mathématiques.

Un anyon forme un espace de Hilbert unidimensionnel, 2 anyons forment un espace de Hilbert à 2 dimensions, et 3 anyons forment un espace de Hilbert à 3 dimensions. C’est ensuite que les choses deviennent intéressantes : 4 anyons forment un espace de Hilbert à 5 dimensions, 5 anyons forment un espace de Hilbert à 8 dimensions, 6 anyons forment un espace de Hilbert à 13 dimensions, et ainsi de suite. Même si le modèle des anyons de Fibonacci semble incroyablement complexe, il constitue en fait le candidat le plus simple que nous connaissions pour l’informatique quantique topologique.

En 2014, des chercheurs de l’Université Cornell et de la station Q de la Division de la recherche de Microsoft ont démontré de manière théorique que, en se déplaçant les uns autour des autres et en traçant des parcours qui forment des tresses et des nœuds, les anyons de Fibonacci deviennent en fait des qubits. Trois ou quatre quasiparticules correspondent à un qubit, et les croisements des chemins correspondent à des portes informatiques.

Comme la démonstration expérimentale de ce qui précède est incroyablement difficile, le physicien théoricien Yidun Wan a proposé une démarche différente. Au lieu d’attendre la découverte d’un système physique permettant de réaliser des anyons de Fibonacci — ce qui pourrait prendre des années — pourquoi ne pas utiliser les capacités actuelles des circuits de calcul quantique pour simuler l’IQT?

Et il savait exactement qui pourrait tester l’idée. L’Institut d’informatique quantique est presque voisin de l’Institut Périmètre, et ses expérimentateurs ont réussi à créer des circuits de 12 qubits entièrement contrôlables. M. Wan était d’avis qu’une démonstration de faisabilité avec 3 qubits serait possible. Il a lancé l’idée lors d’un séminaire de l’IQC, et les expérimentateurs se sont dits d’accord pour essayer.

Se servir des outils disponibles

Dawei Lu, postdoctorant à l’IQC, a consacré la plus grande partie de sa carrière de chercheur aux circuits de calcul quantique. L’idée d’appliquer ces connaissances à l’informatique quantique topologique le fascinait.

Dans un modèle de circuit, on prépare le système pour un certain type de données en entrée, puis on construit des portes par lesquelles passent ces données. L’information est codée au début et décodée à la fin. Dans un système topologique, il faut concevoir les portes selon la manière dont les parcours des anyons se croisent à mesure que le temps s’écoule. Il faut ensuite manipuler les anyons pour qu’ils se déplacent selon les parcours prédéfinis.

Dawei Lu explique que, dans les deux cas, il faut initialiser le système, puis décoder l’information à la fin. D’une manière générale, cela rend les deux systèmes équivalents.

« En autant que je sache, avant ces travaux, les gens considéraient toujours ces deux démarches de manière indépendante », déclare M. Lu, qui occupera à compter du mois d’août un poste de professeur à l’Université méridionale de science et technologie de Shenzhen, en Chine. « Les gens savent que les deux systèmes sont équivalents, mais ils considèrent rarement les liens entre les deux. Ces travaux montrent que, lorsque l’on utilise un modèle de circuit de calcul quantique, cela permet aussi de simuler le modèle topologique. » [traduction]

L’expérience ne visait pas à effectuer des calculs topologiques. Les scientifiques cherchaient plutôt à simuler divers systèmes topologiques et à les distinguer les uns des autres. Dawei Lu dit que l’expérience ressemble à une rencontre avec des triplés identiques : il n’y a pas de moyen immédiat de les distinguer, et il faut donc un examen plus détaillé pour trouver de subtiles différences.

Dawei Lu et le doctorant Keren Li ont préparé 3 systèmes, constitués chacun de molécules de trichloroéthylène à température ambiante qui simulaient des types précis d’ordre topologique (dont l’un était un système d’anyons de Fibonacci non abéliens).

Keren Li, doctorant à l’IQC, et Dawei Lu, postdoctorant à l’IQC, dans le laboratoire où ils ont mis à l’épreuve la théorie de l’IQT[/caption]

À l’aide d’un simulateur quantique à résonance magnétique nucléaire situé dans le bâtiment de chimie de l’Université de Waterloo, les deux chercheurs ont fait faire aux molécules des rotations simulant la manière dont des anyons parcourraient le treillis le plus élémentaire que l’on peut construire sur un tore.

Après chaque rotation, ou « transformation modulaire », ils ont mesuré le nouvel état de base obtenu. En déterminant les produits mathématiques internes qui faisaient passer d’un état de base à un autre, ils ont réussi à construire la matrice déterminant précisément le fonctionnement interne de chaque système.

Les résultats ont révélé des différences précises entre des systèmes qui, au départ, semblaient identiques. Et les résultats de l’expérience correspondaient presque parfaitement aux prédictions théoriques. Les chercheurs avaient trouvé les empreintes digitales identifiant chaque système.

Vers une nouvelle avenue de découvertes

Cela ne constitue que la première étape d’une plus longue recherche en collaboration. Les 3 qubits du modèle de circuit manipulés dans cette expérience ne simulent qu’un seul qubit d’IQT. Pour réellement simuler les excitations dans un système topologique, M. Wan croit qu’il faudra au moins 6 qubits. Le tressage en exigera encore davantage.

Cependant, cette expérience montre que même si l’informatique quantique topologique ne sera peut-être pas réalisable demain, des simulations peuvent aider à trouver une avenue à explorer.

« Je crois qu’il s’agit d’une nouvelle voie vers la réalisation de calculs quantiques, dit M. Wan. Si l’on ne dispose que de 20 qubits et que l’on veut réaliser un circuit de calcul quantique, il est probable que seulement 1 ou 2 qubits servent réellement au calcul quantique. Les autres sont utilisés pour la correction des erreurs. Mais pour la simulation de l’IQT, la plupart des qubits servent au calcul. C’est le meilleur aspect de cette proposition. » [traduction]

La recherche de collaborations comme celle-ci n’est pas typique pour un théoricien comme Yidun Wan, mais ce dernier considère que cela fait partie de ses responsabilités. À son avis, s’il ne cherchait pas à faire en sorte que ses théories soient applicables, leurs conséquences possibles pourraient n’être découvertes que plus tard — sinon jamais.

Il a commencé sa carrière dans le domaine extrêmement abstrait de la gravitation quantique, mais il compte maintenant consacrer une moitié de son temps à la recherche théorique et l’autre moitié à des collaborations avec des expérimentateurs.

« Sans applications, sans expériences, ces choses abstraites n’ont aucun sens pour le monde, dit-il. Je dois trouver de réelles applications physiques. » [traduction]