The greatest achievements of theoretical physics have been feats of unification: Newton's realization that an apple falling to the ground and the Moon orbiting Earth can be explained by one and the same gravitational force; Maxwell’s theory describing electric and magnetic phenomena as different sides of the same coin; Einstein's theory of general relativity fusing together space, time, and gravity; and the discovery — in the context of the standard model of particle physics —that electromagnetism and the weak force are different aspects of a single, more fundamental force called the electroweak force. String theory is an attempt to complete the quest for unification: to formulate all the laws of physics within a single mathematical framework.
String Theory 101
The basic idea of string theory is simple. According to particle physics, there are a fairly large number of elementary constituents — building blocks from which everything is constructed: the electron, the photon, the quarks, and so forth. As far as experiments can tell, all these particles are point-like, or zero-dimensional — they have no spatial extent at all. According to string theory, on the other hand, there is only one elementary constituent: a tiny, one-dimensional "string," which can either have both its ends free, called an open string, or both its ends joined to form a loop, called a closed string. In simplified form, these can be pictured as shown in the figure below.
How might an elementary string account for all known elementary particles? Again, the basic idea is simple: an elementary string, open or closed, can oscillate in many different ways, similar to the strings of a guitar or violin. Just as different oscillations of a musical string produce notes of different pitch, and combinations produce tones of different timbre, different oscillations of an elementary string correspond to different values for the physical properties of the string, such as its mass or spin.
To get a feel for how this works, let's recall that in the quantum world there is a close relationship between the frequency with which something oscillates, and its energy. Einstein provided the first example, suggesting that the energy of a quantum of light — a photon — is related to its colour, or frequency of oscillation: the higher the frequency, the higher the energy. Moreover, in Einstein’s relativistic world, there is also a relationship between energy and mass: E = mc2. If we combine these two relationships, we see that in a world that is both quantum and relativistic (our world), there is a close relationship between the frequency with which something oscillates — an elementary string in our case, and its physical mass, i.e., the mass of the elementary particle it is mimicking. Thus, the different elementary particles we see — the electron, the photon, the quarks, and so on — may all be the same entity: an elementary string, just singing different notes. This potential to unify particle physics is one of the very compelling aspects of string theory.
If string theory is true, why have our most detailed probes of the elementary particles never revealed any such "stringy" structure? Why do we see only point-like entities? The answer is simple: elementary strings, if they exist, are far too tiny to see. It is unlikely that even the most sophisticated microscope or particle accelerator that could be constructed would ever have enough resolution to directly "see" the strings of string theory. This is similar to the fact that we typically do not see the individual pixels on our computer screen when looking at it. They are simply too small. We must be clever and find convincing indirect evidence.
Why all the interest in string theory?
Besides the potential to unify particle physics, there are several other reasons string theory is extremely intriguing.
For one thing, it is naturally free of the sort of "infinities" that plagued particle physics in the mid-twentieth century. Consider two electrons, which repel because they have a like charge. The closer they are, the greater the repulsive force. If electrons are truly point particles, they can be brought infinitely close together, resulting in an infinite repulsive force. It turns out this property of point particles wreaks havoc with trying to extract sensible predictions from the theory. Eventually, a "fix" was found for this, but one that works well for only three of the four fundamental forces of nature; it works also for the fourth force, gravity, but only when gravity is so weak that it can be neglected. A significant new idea is needed.
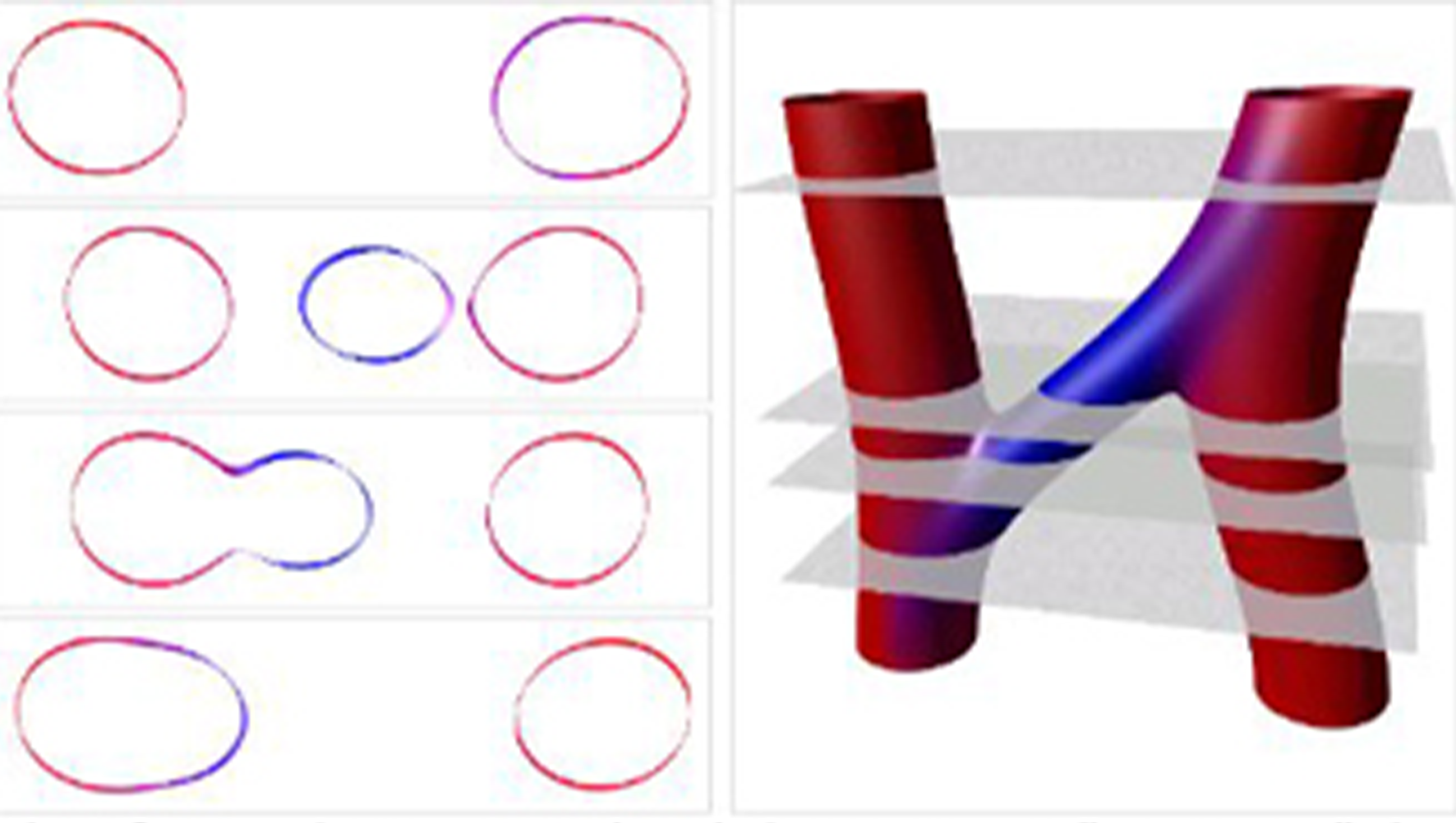
String theory does not have this problem of infinities, because strings are extended objects. For example, two nearby strings may "interact" by exchanging a third string, as shown in the figure. This interaction is spread out smoothly over space and time, and there are no nasty infinities.
Moreover, there is one particular oscillation of the closed string, which must occur in every well-behaved (mathematically self-consistent) string theory and has just the right properties to give a sensible quantum mechanical description of the gravitational attraction between matter particles. This is an extraordinary property of string theory, for after all, formulating a theory of quantum gravity is widely seen as the most important open problem in theoretical physics. String theory automatically contains a theory of quantum gravity! Whether it is the correct theory of quantum gravity is still not known.
Another amazing feature of string theory is that, in order for an elementary string to be able to mimic both force particles (photon, gluon, etc.) and matter particles (electron, quarks, etc.), the theory makes a definite prediction about the types of particles that must exist in nature. Roughly speaking, for every type of force particle, there must exist a type of matter particle with certain properties, and vice versa. For example, corresponding to the photon, there must exist a matter particle called a photino; corresponding to the electron, there must exist a force particle called the selectron. This hypothetical relationship between force and matter particles is called "supersymmetry," and is what the "super" means in "superstring" theory (which is what string theory is sometimes called). While no experimental evidence has yet been found for such supersymmetric partner particles, this might simply be because all such particles are too massive to have been produced (and observed) in any previous particle accelerator. This is one reason why there is such excitement about the Large Hadron Collider (LHC) recently constructed at CERN. The hope is to discover evidence for supersymmetry, which would bolster the case for superstring theory.
Perhaps the most astounding property is that, in string theory, physicists found a theory of nature so deep that it is able to make a prediction about something at the very foundations of the structure of the universe. Not just a prediction about things that may or may not exist in spacetime, but a fundamental prediction about spacetime itself, namely, the number of dimensions it must have. This is unprecedented. It should be added that this prediction is intimately connected with the quantum nature of the universe. In contrast, Einstein's theory of general relativity — our best (non-quantum) theory of space, time, and gravity — works just as well in 4 spacetime dimensions as in 24. It has no preference. String theory, on the other hand, works in only a certain number of spacetime dimensions: 10 (or 11, depending on how you look at it). Whether this prediction of spacetime dimension is correct or not is beside the point. It's significant because it raises hope that a mathematical description of nature, with a predictive power sufficient to be called a "theory of everything," may very well exist.
Where are the extra dimensions?
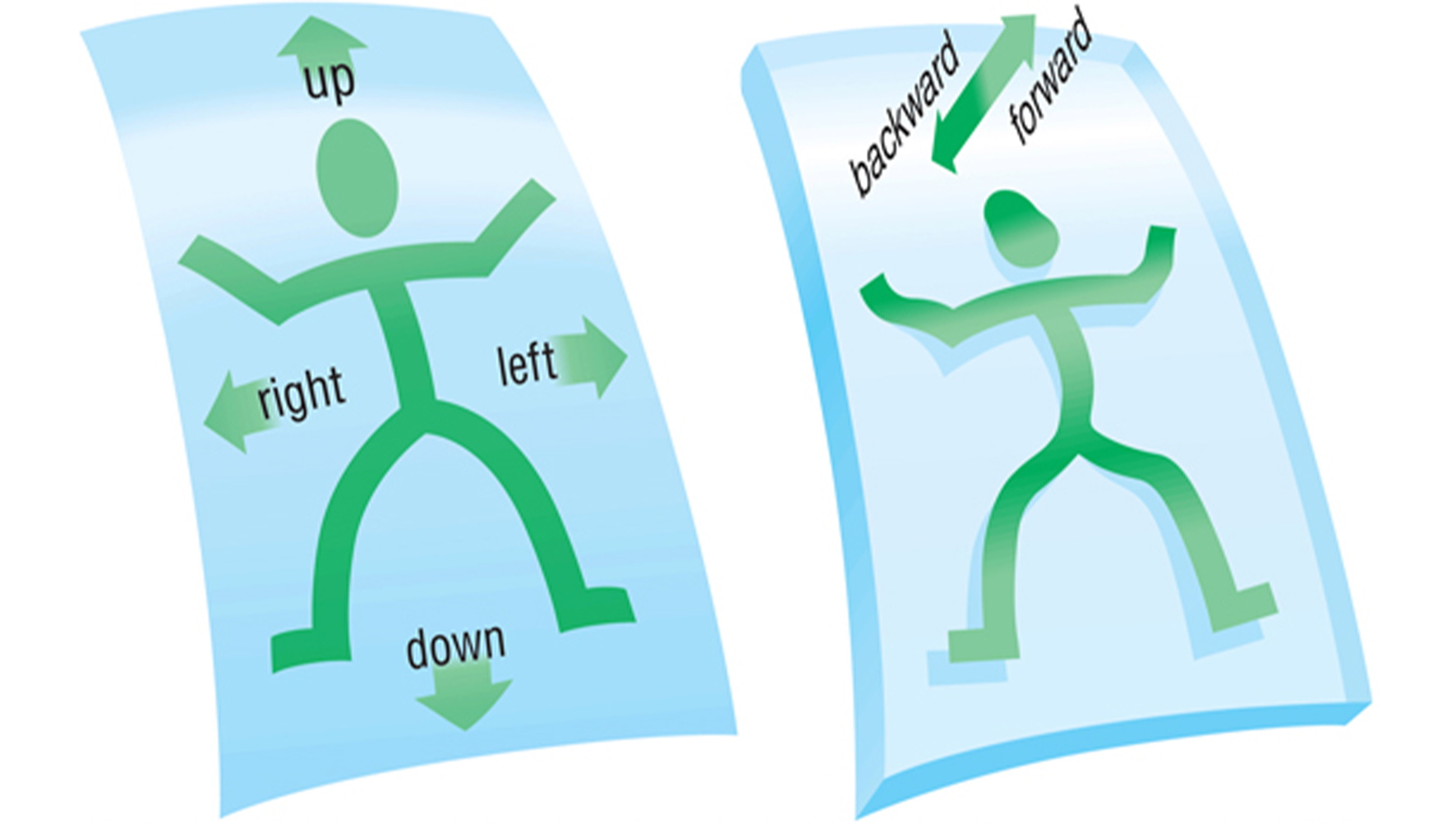
As to the correctness of the prediction, that’s another matter. On the surface, it appears to be dead wrong. There are "obviously" only 3 space dimensions, not 9. But the situation is considerably more subtle (and delightful) than this. Perhaps the extra 6 dimensions are simply "small" enough to have escaped our notice. To see how this might be possible, imagine that, instead of 3-dimensional beings living in a 3-dimensional space, we are 2-dimensional beings living in a 2-dimensional space, as shown in the figure. All of our movements are confined to up-down and left-right; there is no such thing as forward-backward. One day, a magician arrives who makes our world 3-dimensional by slightly "thickening" it in the forward-backward direction. If the additional freedom of motion this affords us were sufficiently small compared to the size of our bodies, our new freedom would be imperceptible to our senses. String theorists have in mind something like 10–35 m, which is clearly in the "sufficiently small" category, even for the most precise experiments we could imagine!
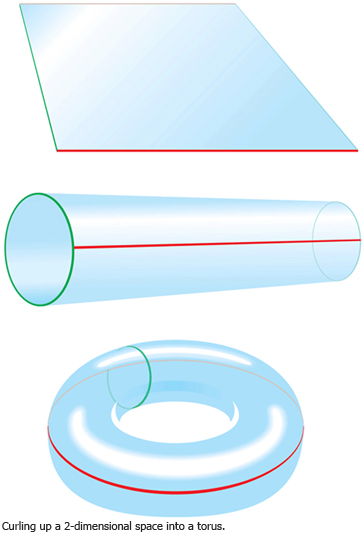
Moreover, such extra spatial dimensions would be "curled up." In our previous example, we had only one extra dimension: movement forward or backward a short distance. If we represent this dimension of movement as a short line segment, we can curl it up by connecting the two ends of the segment, thus forming a circle. Now when we move forward, instead of encountering a boundary — the "end of space" — we simply re-emerge into the same space from the other end — a finite-sized space, but with no boundary! With two extra dimensions, we begin with a two-dimensional square instead of a one-dimensional line segment (see figure). If we connect its front and back edges, we get a cylinder; then connecting the remaining left and right edges gives us a torus (donut), as shown.
Again, we have a finite-sized space with no boundary. With 6 extra dimensions, there are many ways to curl them up; the figure below attempts to illustrate the potential complexity.
In addition to the elementary string oscillations discussed above, the precise way in which these extra dimensions are curled up affects the predictions string theory makes regarding the kind and properties of the elementary particles we observe in our familiar 4-dimensional spacetime. On a positive note, this increases the possibility that at least one of these ways will yield the properties of the elementary particles we know. The problem is that string theory does not seem to prefer one way over another. In other words, nature has many choices, but why she made the choice she did might be beyond string theory to explain.
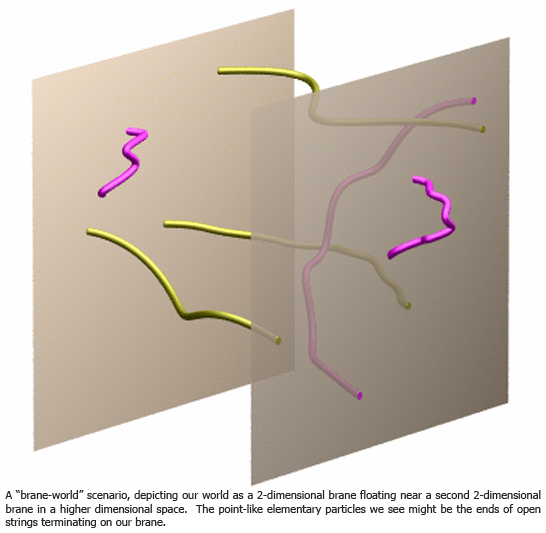
At the other extreme, these 6 extra dimensions might be "large." Our 3-dimensional world might be floating through a 9-dimensional space, like a 2-dimensional sheet of paper through 3-dimensional space. In fact, string theory predicts the existence of extended objects called branes (short for "membranes"), which can have zero dimensions (like particles), one dimension (like the elementary strings), or any other number up to the number of space dimensions itself. Our world could be a 3-dimensional brane, and what we detect as point-like elementary particles could be the ends of open strings that are trapped on the brane. Below is a schematic depiction of our world brane (shown as a 2-dimensional surface) floating through a higher (three)-dimensional space, with another brane right behind it.
Might it be possible to somehow detect such large extra dimensions? By definition, we — and all of our measuring instruments — are confined to our 3-dimensional world brane, and so it would seem the answer is no. But it could be yes. One idea is that gravity, which has always been an "outsider" to the particle physics world, might be an outsider quite literally. Unlike the other three fundamental forces, which, along with matter, are confined to the brane, gravity might live in the higher-dimensional space such that a nearby brane world could affect our brane world via gravity. Perhaps our experience of gravity is like the shadows in Plato’s famous allegory of the cave. Remarkably, there may be a measurable signature of this fantastic scenario, and experimental research is currently underway!
In another spectacular demonstration of its potential, string theory has led to a possible concrete realization of the holographic principle, called the Maldacena conjecture. Proposed by Gerard 't Hooft and Leonard Susskind, the basic idea of the holographic principle is that in order for quantum theory and Einstein’s theory of gravity to coexist in our universe, there must be much less information about what’s physically happening inside any given 3-dimensional volume of space (e.g., objects moving this way and that) than we had previously expected. In fact, the amount cannot exceed what we would expect of a physical reality existing in a 2-dimensional surface — the surface bounding that volume. While it's a bit subtler than this, it's nevertheless quite analogous to the way the information in a 3-dimensional scene can be stored in a 2-dimensional hologram. In the context of string theory, Juan Maldacena discovered connections of exactly this sort between certain physical theories in different numbers of dimensions.
Summary
String theory is, if nothing else, certainly a mathematically rich theory that has had considerable impact on many areas of mathematics. For instance, the study of the different ways the extra dimensions can be curled up has led to important new insights into exotic types of geometry of great interest to pure mathematicians.
It is also a potentially very rich theory from a physics perspective. It touches deeply on many aspects of the universe, ranging from the building blocks of all matter and radiation to the dimensions of spacetime, the quantum nature of gravity, and even the holographic principle.
But mathematical elegance and tantalizing physical insights, as deep as they may be, are not enough. To be successful, string theory needs to be related to observations and testable predictions. Like many other theories of quantum gravity, most of its predictions are currently not accessible by present-day experiments. However, string theory is young. Researchers are still trying to understand various ways of testing it to see if it matches reality. One promising line of research that may produce testable predictions relates string theory to cosmology. For example, researchers are trying to understand if string theory might be able to explain inflation in the early universe, and if so, what observational signatures this might have left behind.
If, one day, string theory is confirmed by experiments, scientists will have found what is arguably the "holy grail of physics": a single theory that describes the nature of the universe at the most fundamental level.
Quantum fields and strings researchers
-

-

Freddy Cachazo
Research Faculty
Office of Executive Leadership
Deputy Director (Interim)Mathematical PhysicsQuantum Fields and Strings -

Robert Myers
Research Faculty
Perimeter Research Chair
Director EmeritusBMO Financial Group Isaac Newton Chair in Theoretical PhysicsQuantum Fields and Strings -

Davide Gaiotto
Research Faculty
Perimeter Research Chair
Krembil Galileo Galilei Chair in Theoretical PhysicsMathematical PhysicsQuantum Fields and Strings -

-

Alex May
Research Faculty
Perimeter Research Chair
Murray Gell-Mann Chair in Theoretical PhysicsQuantum Fields and StringsQuantum Information -
Pedro Vieira
Research Faculty
Perimeter Research Chair
The Clay Riddell Paul Dirac Chair in Theoretical PhysicsMathematical PhysicsQuantum Fields and Strings -

Robert Myers
Research Faculty
Perimeter Research Chair
Director EmeritusBMO Financial Group Isaac Newton Chair in Theoretical PhysicsQuantum Fields and Strings -

Davide Gaiotto
Research Faculty
Perimeter Research Chair
Krembil Galileo Galilei Chair in Theoretical PhysicsMathematical PhysicsQuantum Fields and Strings