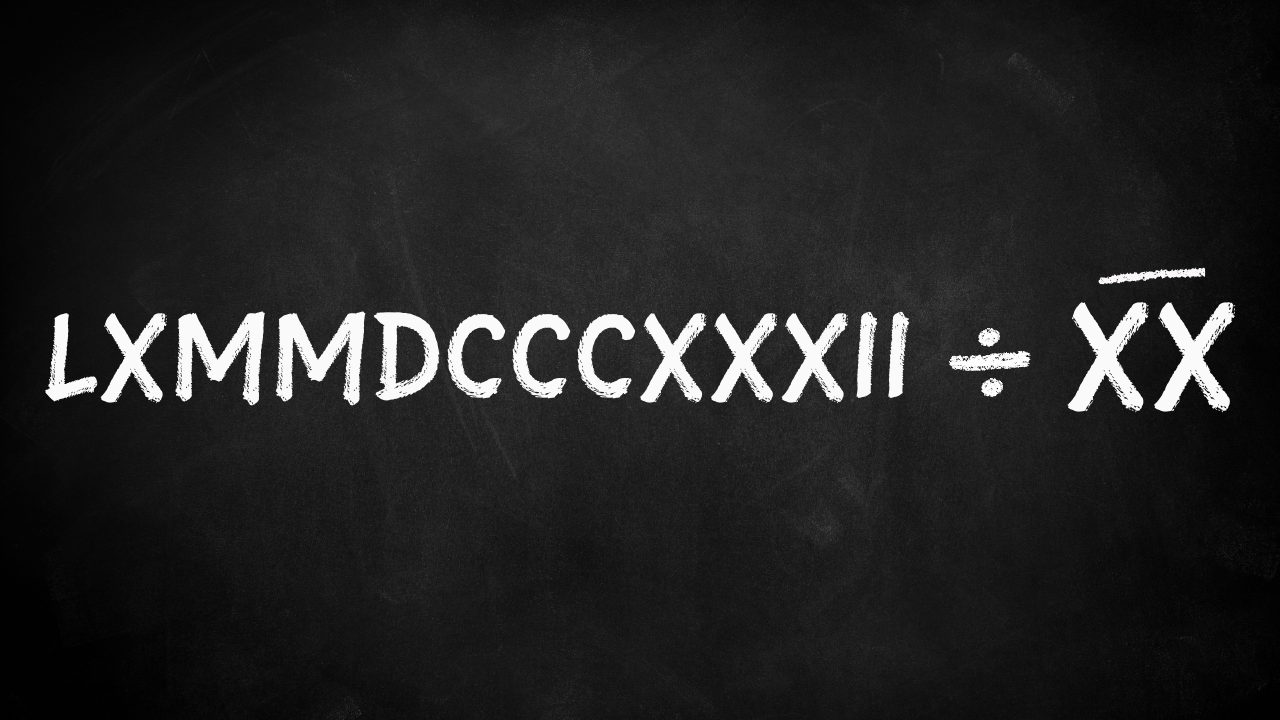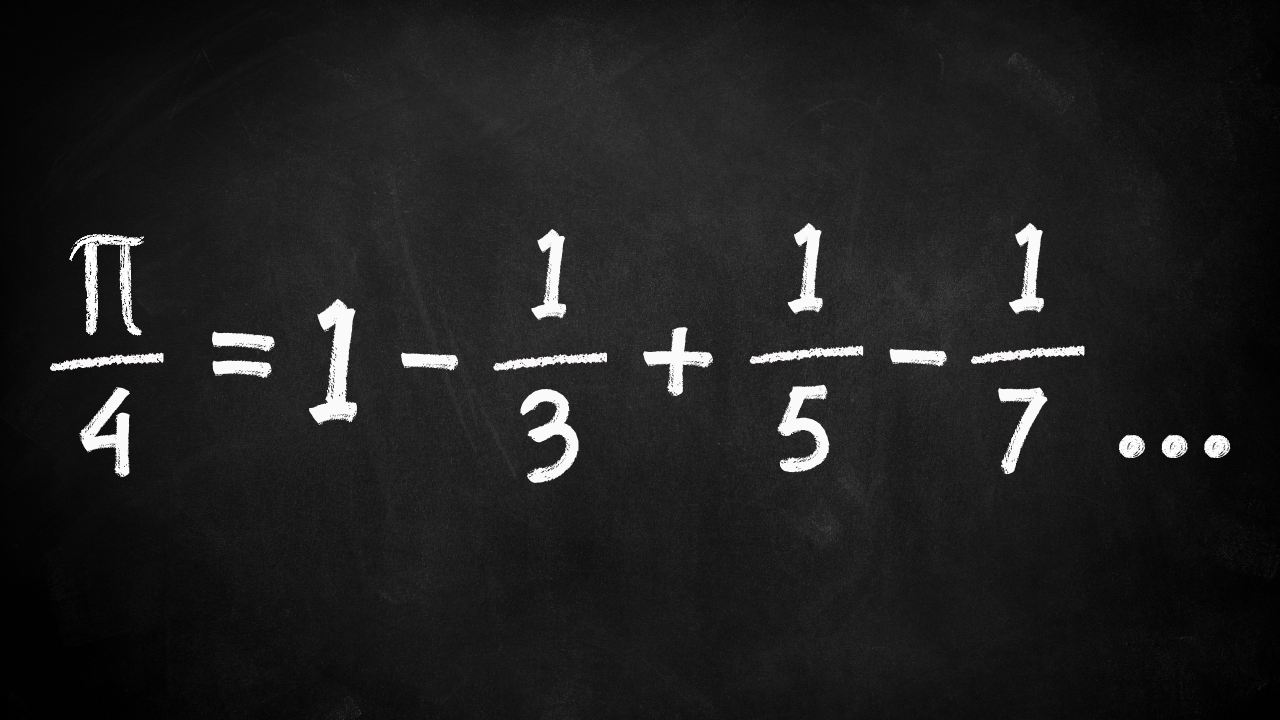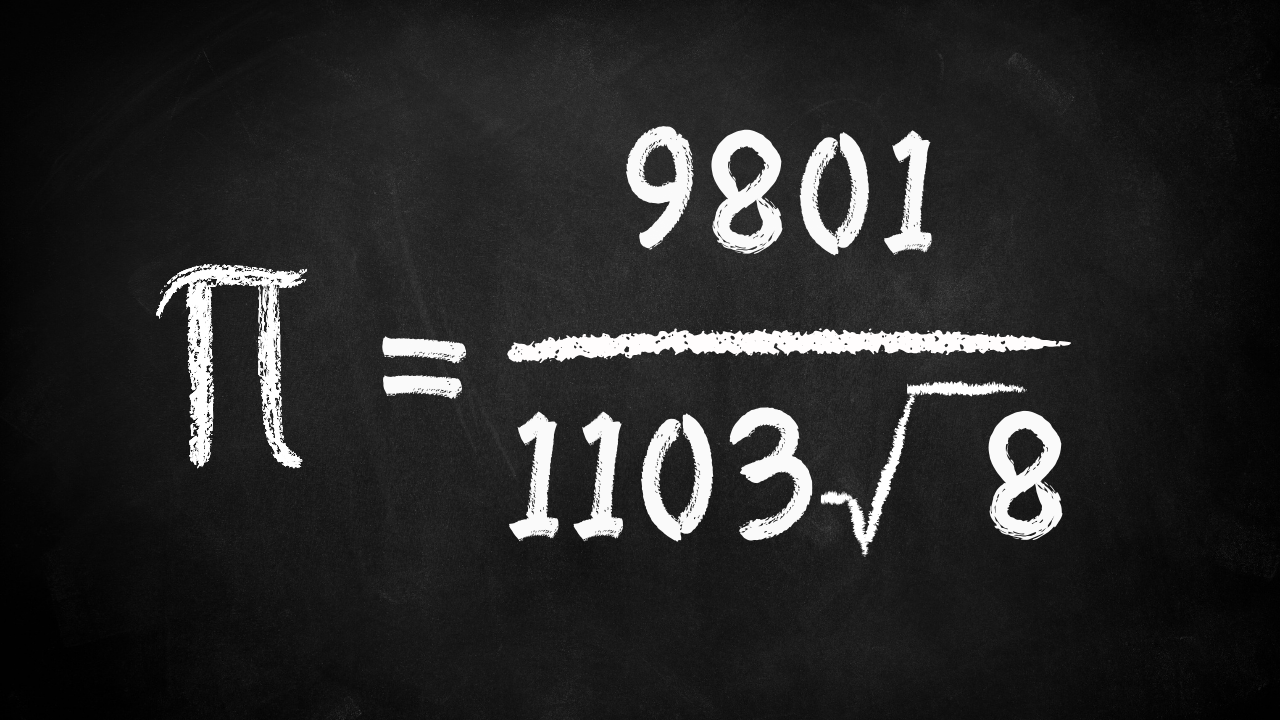Pi. 3,1415. π. Le rapport entre la circonférence d’un cercle et son diamètre. C’est le nombre irrationnel le plus célèbre de tous – et il fascine les mathématiciens depuis des millénaires.
L’histoire de pi – une quête vieille de 4 000 ans pour en découvrir toujours plus de décimales – nous entraîne de la Babylone antique à l’ère des superordinateurs. Ce récit est presque aussi long que pi lui-même, et nous fait voyager des greniers mésopotamiens aux écoles secondaires américaines, avec une bonne douzaine de détours en chemin. Attachez votre ceinture : on remonte le temps pour découvrir l’origine du nombre le plus savoureux de toutes les mathématiques.
3,14 : l’aube de pi
Notre histoire commence à l’apogée de l’une des premières grandes civilisations humaines : la Babylone antique. Centre agricole florissant grâce au commerce, Babylone était un lieu de prospérité et de changement. Les sociétés mésopotamiennes qui l’avaient précédée avaient déjà introduit des avancées comme l’écriture, les systèmes numériques et d’audacieuses innovations comme les fractions. Mais c’est le système de numération basé sur les comptes de Babylone, ainsi que l’invention de l’abaque, qui ont permis d’accélérer les calculs de manière spectaculaire.
Une société plus complexe nécessitait des mathématiques plus complexes – et ce n’est pas long avant qu’un ratio pratique pour les cercles devienne essentiel. C’est plus facile de taxer la population, de comptabiliser les ressources ou de planifier la construction de greniers cylindriques quand on dispose de constantes comme pi.
Les premières traces connues de pi remontent à environ 2000 av. J.-C. Elles montrent que les Babyloniens considéraient généralement que pi était égal à trois. Mais une tablette d’argile découverte dans les années 1930 révèle qu’au moins une personne ambitieuse avait estimé pi à environ 25/8, soit 3,3125.
Environ 500 ans plus tard, dans une autre civilisation florissante sur les rives du Nil, un scribe égyptien du nom d’Ahmès a franchi une nouvelle étape importante. Un papyrus conservé à ce jour, rempli de calculs et de problèmes mathématiques, nous donne un aperçu des connaissances mathématiques à son époque. On y voit que l’Égypte avait perfectionné l’usage des chiffres et des fractions, ce qui a permis à Ahmès d’estimer pi à environ 256/81, soit 3,16.
Le dernier grand progrès de cette période ancienne vient de l’Inde, vers 800 av. J.-C. Des érudits religieux cherchaient alors à normaliser la construction d’autels de formes variées (cercles, demi-cercles, carrés) devant occuper la même superficie. En utilisant des cordes et des briques pour « quadrer le cercle », ils se référaient souvent, comme les Babyloniens, à une valeur arrondie de trois – mais leurs meilleures estimations atteignaient 3,138.
À ce moment-là, l’humanité n’a même pas encore inventé la selle, mais on a déjà calculé pi avec une précision de 1 %. Pas mal!
3,1415 : Quadrature (et polygones) du cercle
En Grèce, vers 250 av. J.-C., un mathématicien du nom d’Archimède a compris qu’un pentagone permettrait une meilleure approximation de pi qu’un carré – et qu’un hexagone ferait encore mieux, et ainsi de suite.
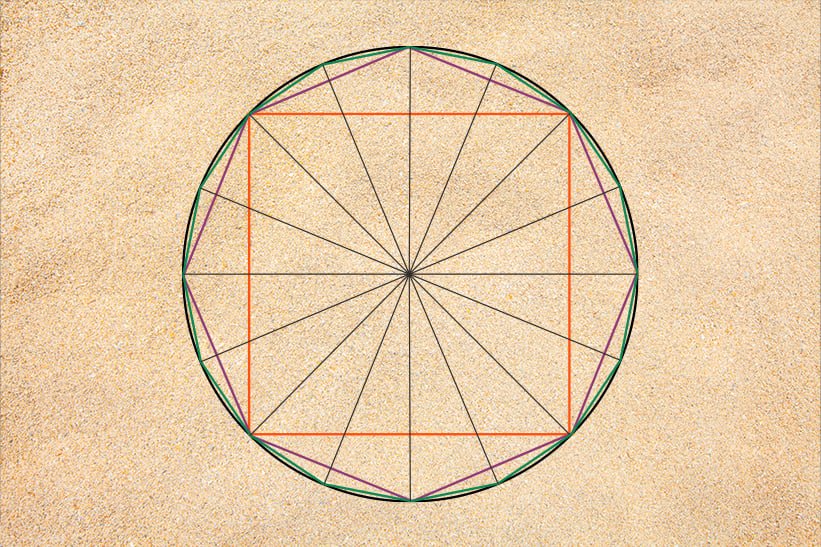
L’approximation d’Archimède est appelée la « méthode d’exhaustion », car les mesures et les calculs étaient extrêmement longs. Il a commencé par dessiner un cercle et y a inscrit un carré dont les coins touchaient tout juste le cercle. Ensuite, il a dessiné un carré circonscrit dont les côtés touchaient l’extérieur du cercle. Si l’on additionne les longueurs des côtés de chaque carré et qu’on les divise par une mesure diagonale correspondante, on obtient deux valeurs – entre lesquelles se trouve pi.
Archimède a ensuite remplacé les carrés par des pentagones, puis a répété le processus. Les nouvelles valeurs calculées s’approchaient encore davantage de pi. Il a continué à doubler le nombre de côtés de ses polygones jusqu’à atteindre 96 côtés, et a déterminé que pi se situait entre 3 1/7 (3,1429) et 3 10/71 (3,1408).
Selon la légende, Archimède était encore en train de calculer ses cercles lorsque sa ville fut envahie par les Romains. Ses derniers mots, avant d’être tué, auraient été : « Ne dérangez pas mes cercles! »
À peu près à la même époque, le mathématicien chinois Liu Hui a mis au point le premier algorithme rigoureux pour calculer pi – une méthode qui allégeait un peu l’éreintante méthode d’exhaustion. Comme Archimède, Liu Hui utilisait des polygones pour ses calculs. Dans sa méthode, il plaçait un hexagone à l’intérieur du cercle (voir diagramme), le coupait en deux, puis le divisait en une série de triangles. Ensuite, il utilisait le théorème de Pythagore – encore et encore – pour générer de nouveaux triangles, qui lui permettaient d’affiner son approximation. Grâce à cet algorithme itératif, Hui est parvenu à une estimation de pi à cinq décimales : 3,1416.
Hui a conclu que 3,14 était une estimation suffisante pour la plupart des usages. D’autres mathématiciens chinois n’étaient pas du même avis. Deux siècles plus tard, Zu Chongzhi a utilisé cette méthode pour calculer que pi se situait entre 3,1415926 et 3,1415927 – un record de précision qui est resté inégalé pendant plusieurs siècles.
La prochaine grande avancée dans l’histoire de pi n’a pas ajouté de nouvelles décimales, mais elle a rendu les calculs beaucoup plus efficaces. Au 6e siècle de notre ère, un mathématicien, astronome et pionnier de la physique du nom d’Aryabhata, né en Inde, a déclaré : « Ajoutez quatre à cent, multipliez par huit, puis ajoutez 62 000. Cette règle permet d’approcher la circonférence d’un cercle de 20 000 de diamètre. » Ce qui revient essentiellement à 62832 ÷ 20000, ou 3,1416.
On ne sait pas exactement comment Aryabhata a trouvé ces chiffres, mais on sait qu’ils utilisaient un système de numération à valeur de position – un système où la valeur d’un chiffre dépend de sa position dans le nombre (comme le 30 qui signifie trois groupes de dix). Cela rend les calculs beaucoup plus rapides. Imaginez devoir faire 62832 ÷ 20000 uniquement avec des chiffres romains. Pour mémoire, cela donnerait :
3,14159265359 : pi prend son envol
Pendant environ 700 ans, pi est resté relativement inchangé – jusqu’à ce qu’un autre mathématicien indien, Madhava de Sangamagrama, découvre davantage de décimales grâce à la puissance des séries infinies.
On en sait peu sur Madhava. Né vers 1340 de notre ère, les connaissances que nous avons sur lui proviennent surtout des écrits de ses élèves. Parmi ses nombreuses innovations mathématiques, on compte l’utilisation de séries infinies pour approximer différentes fonctions trigonométriques.
Madhava a compris qu’en additionnant et en soustrayant successivement certaines fractions à numérateur impair, on pouvait obtenir une bien meilleure estimation de pi. Cela donnait quelque chose comme ceci :
Madhava a également conçu une correction qui lui a permis de calculer pi jusqu’à la 11e décimale, soit 3,14159265358. La série serait redécouverte 300 ans plus tard en Europe, sous le nom de formule de Leibniz. Aujourd’hui, on parle souvent de la formule de Madhava-Leibniz pour souligner la contribution essentielle de Madhava.
Le prochain grand bond en avant a eu lieu à peine un siècle plus tard, grâce au mathématicien perse Jamshid al-Kashi, en 1424. Dans ses écrits, il fait référence à Archimède et semble avoir porté la méthode d’exhaustion à un tout autre niveau. Munis d’un meilleur système numérique et de nouvelles méthodes pour travailler les fractions, Al-Kashi est parvenu à calculer pi avec un record de 16 décimales : 3,14159265358979323.
Les séries infinies ont finalement fait leur entrée en Europe en 1593, lorsque François Viète a publié la première formule de ce type dans les mathématiques européennes. Au cours des 300 années suivantes, les Européens ont continué d’ajouter des décimales grâce aux séries infinies et à des améliorations progressives de la méthode d’exhaustion d’Archimède.
En 1654, Christiaan Huygens a utilisé ce qu’on appellera plus tard l’extrapolation de Richardson pour raccourcir les inégalités de la méthode d’Archimède. En utilisant le centre de gravité d’un segment de parabole, qu’il a ensuite appliqué aux cercles, il a pu obtenir des approximations plus rapides et plus précises.
À partir de là, pi a explosé. Dans les années 1670, James Gregory et Gottfried Leibniz ont tous deux utilisé la série de Madhava-Leibniz pour calculer encore plus de décimales. En 1706, John Machin a atteint les 100 premières décimales de pi grâce à une variante de la série Madhava-Leibniz combinée au développement en série de Taylor (nommée d’après Brook Taylor, mais découverte par Madhava dans les années 1300).
La même année, un proche d’Isaac Newton nommé William Jones a commencé à utiliser le symbole π pour représenter pi – une abréviation pratique du mot grec περιφέρεια (periphéreia, ou périphérie). Dans les années 1760, Johann Heinrich Lambert a démontré que pi est un nombre irrationnel.
Malgré les progrès en efficacité, les calculs demeuraient fastidieux et vulnérables aux erreurs humaines. Par exemple, William Rutherford a calculé 208 décimales de pi au XIXe siècle, mais seulement 152 étaient exactes. William Shanks est allé jusqu’à 707 décimales en 1873 – mais seules les 527 premières étaient correctes. Peu importe les erreurs, les mathématiciens étaient désormais capables de pousser pi jusqu’à plusieurs centaines de chiffres.
Mais une invention allait tout changer, faisant passer pi de centaines de décimales… à des milliards.
L’ordinateur.
Jusqu’à 3,1415926535897932384626433832795028841 et au-delà
Avec l’invention de l’ordinateur, la course s’est emballée : en moins de 80 ans, on a franchi le cap des billions de décimales.
C’est probablement bien plus que ce dont nous aurons jamais besoin. Pour donner un peu de perspective, il suffit d’utiliser pi jusqu’à la 38e décimale pour calculer la circonférence d’un cercle de la taille de l’univers… avec une précision équivalente à la taille d’un atome d’hydrogène, selon Marc Rayman, ingénieur en chef des opérations scientifiques à la NASA, au Jet Propulsion Laboratory. Mais la recherche d’utilité n’a jamais arrêté les mathématiciens et les spécialistes en informatique – bien au contraire.
La méthode actuelle pour calculer de nouvelles décimales de pi repose sur les travaux du mathématicien indien Srinivasa Ramanujan, né en 1887. En explorant les séries infinies, Ramanujan a découvert certaines expressions mathématiques qui, combinées, permettaient une convergence bien plus rapide et efficace :
Ramanujan n’a jamais expliqué comment il avait trouvé cette formule – ni pourquoi il avait choisi les nombres 9801 et 1103 – mais son équation est incroyablement efficace. Un seul terme suffit à calculer six décimales de pi. À titre de comparaison, la série de Madhava-Leibniz nécessite plus de 1,4 million de termes pour atteindre le même niveau de précision.
La série de Ramanujan est devenue la base de tous les algorithmes informatiques les plus rapides pour calculer de nouvelles décimales de π au cours des cinquante dernières années. En 1988, les frères Chudnovsky ont publié un algorithme basé sur sa formule qui a permis de calculer pi jusqu’à sa milliardième décimale. Depuis, les chercheurs japonais Yasumasa Kanada et Daisuke Takahashi ont établi 11 des 21 records mondiaux de calcul de pi à l’aide de cet algorithme.
La plus récente grande innovation dans le calcul de pi s’appelle y-cruncher, un logiciel conçu par le développeur américain Alexander Lee, à partir d’un projet qu’il a commencé au secondaire. Bien qu’il ait été initialement créé pour calculer la constante d’Euler-Mascheroni, y-cruncher a été utilisé dans tous les records de calcul de pi depuis – y compris le plus récent.
En juin 2024, Jordan Ranous, Kevin O’Brien et Brian Beeler ont calculé la 202 112 290 000 000e décimale de pi (c’est un 2, si vous vous posez la question).
Pourquoi pi?
À ce stade, nous avons bien plus de décimales que nous saurions utiliser. Pi jusqu’à la 202 000 milliardsième décimale n’est sans doute pas très utile pour calculer des cercles, mais cela reste précieux en informatique. D’abord, le calcul de pi constitue un excellent banc d’essai pour évaluer la puissance de calcul. Ensuite, la répartition apparemment aléatoire et uniforme de ses chiffres en fait un bon générateur de nombres pseudo-aléatoires. Mais même là, 200 000 milliards, ça semble beaucoup.
Alors pourquoi faire tout ça? Le youtubeur Simon Clark l’a peut-être mieux résumé : « Les humains sont bizarres. On aime comprendre le monde qui nous entoure et, au fil du développement de notre civilisation, on a construit des outils de plus en plus complexes pour y parvenir. Ce n’était pas essentiel à notre survie… on l’a juste fait, parce que c’est dans notre nature. »
Des premières estimations faites à l’aide de simples entailles, à la construction d’autels et de greniers, jusqu’aux limites des algorithmes modernes, pi reste un objet que l’on peut toujours pousser plus loin. C’est presque un défi inscrit dans la nature elle-même : « Je te défie… si tu en es capable. »
À propos de l’IP
L'Institut Périmètre est le plus grand centre de recherche en physique théorique au monde. Fondé en 1999, cet institut indépendant vise à favoriser les percées dans la compréhension fondamentale de notre univers, des plus infimes particules au cosmos tout entier. Les recherches effectuées à l’Institut Périmètre reposent sur l'idée que la science fondamentale fait progresser le savoir humain et catalyse l'innovation, et que la physique théorique d'aujourd'hui est la technologie de demain. Situé dans la région de Waterloo, cet établissement sans but lucratif met de l'avant un partenariat public-privé unique en son genre avec entre autres les gouvernements de l'Ontario et du Canada. Il facilite la recherche de pointe, forme la prochaine génération de pionniers de la science et communique le pouvoir de la physique grâce à des programmes primés d'éducation et de vulgarisation.