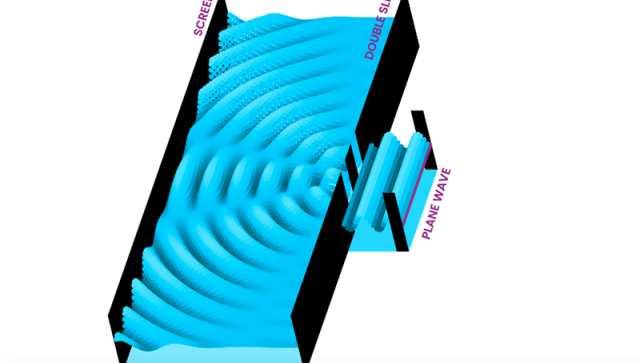
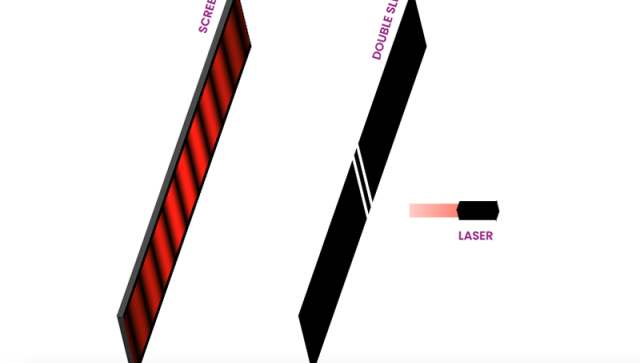
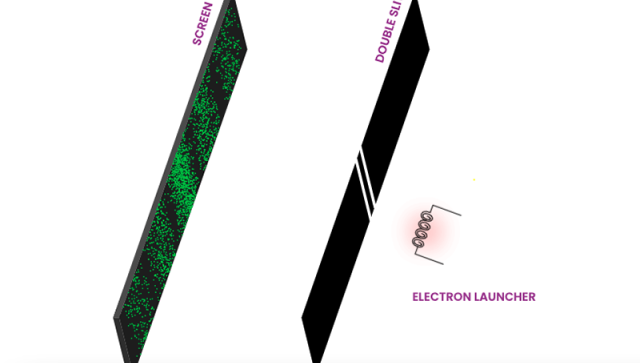
Double-slit experiment simulations
Students can explore the double-slit experiment and investigate the nature of classical particles, classical waves, light, and electrons through this series of four simulations. The simulations can be used to illustrate the results of the experiment in each case and advanced controls allow the user to modify the screen distance, slit separation, wavelength, and energy. The simulations are related to Activity 4 in The Challenge of Quantum Reality classroom resource, available to download for free from our Resource Centre.
Quantum Nature of Light
Students can explore the quantum nature of light through these simulations that illustrate how the behaviour of light cannot be explained solely with a classical, wave model. The simulations can be used for online teaching and are related to our Investigating Planck's Constant with LEDs classroom resource, available to download for free from our Resource Centre.
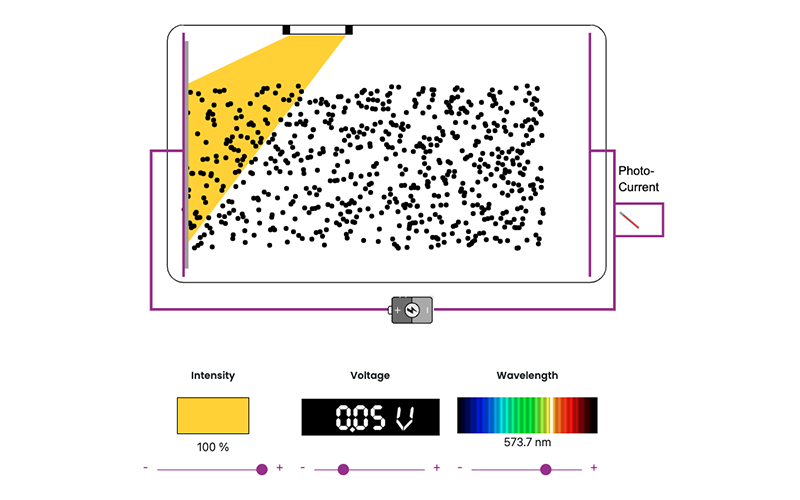
Photoelectric effect
Students will observe light waves behaving like particles as they investigate how the kinetic energy of electrons ejected from a metal surface is related to the frequency of incident light. Students can use data collected from the simulation to create a graph of the kinetic energy of the electrons versus the frequency of light. The maximum kinetic energy of the ejected electrons is found by measuring the reverse potential difference applied across the phototube that stops the flow of ejected electrons (cutoff potential).
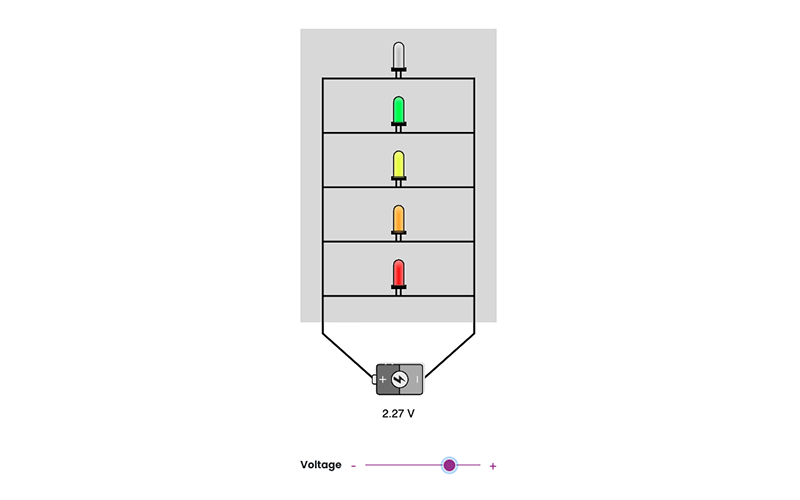
LEDs and Planck’s Constant
Students can observe LEDs in a simple circuit and make measurements to determine Planck’s constant, a fundamental and important constant in quantum mechanics. Students can adjust the settings to find the threshold voltage - the voltage where the LEDs just start to light up. A graph of the voltage versus the frequency of light will allow them to determine Planck’s constant using e∆V=hf .
.
Resources & opportunities

Poster gallery
Resources playlist

Quantum to Cosmos

Scavenger Hunt - Elementary

Can You Build a Quantum Computer? Interactive Activity

Scavenger Hunt - High School

Educational Resources

Tools for Teaching Science