Structure du programme
Le programme comporte 2 phases de cours qui se chevauchent et un bref projet de recherche donnant lieu à un mémoire.
- Cours obligatoires : sujets fondamentaux — physique classique, mécanique quantique, relativité, théorie quantique des champs, physique statistique, physique mathématique, méthodes numériques (4 sessions de 5 semaines chacune, pendant lesquelles 2 cours sont donnés en parallèle).
- Cours au choix : sujets de disciplines précises — telles que physique des particules, cosmologie, information quantique, fondements quantiques, physique de la matière quantique — et cours sur des domaines spécialisés qui constituent des sujets de l’heure, par exemple apprentissage automatique pour la physique des systèmes à N corps et correspondance AdS/CFT. Les étudiants doivent suivre au moins 6 cours au choix.
Chaque étudiant entreprend un bref projet de recherche, sous la direction d’un professeur de l’Institut ou d’une université partenaire, et rédige un mémoire qui est présenté et soutenu devant public.
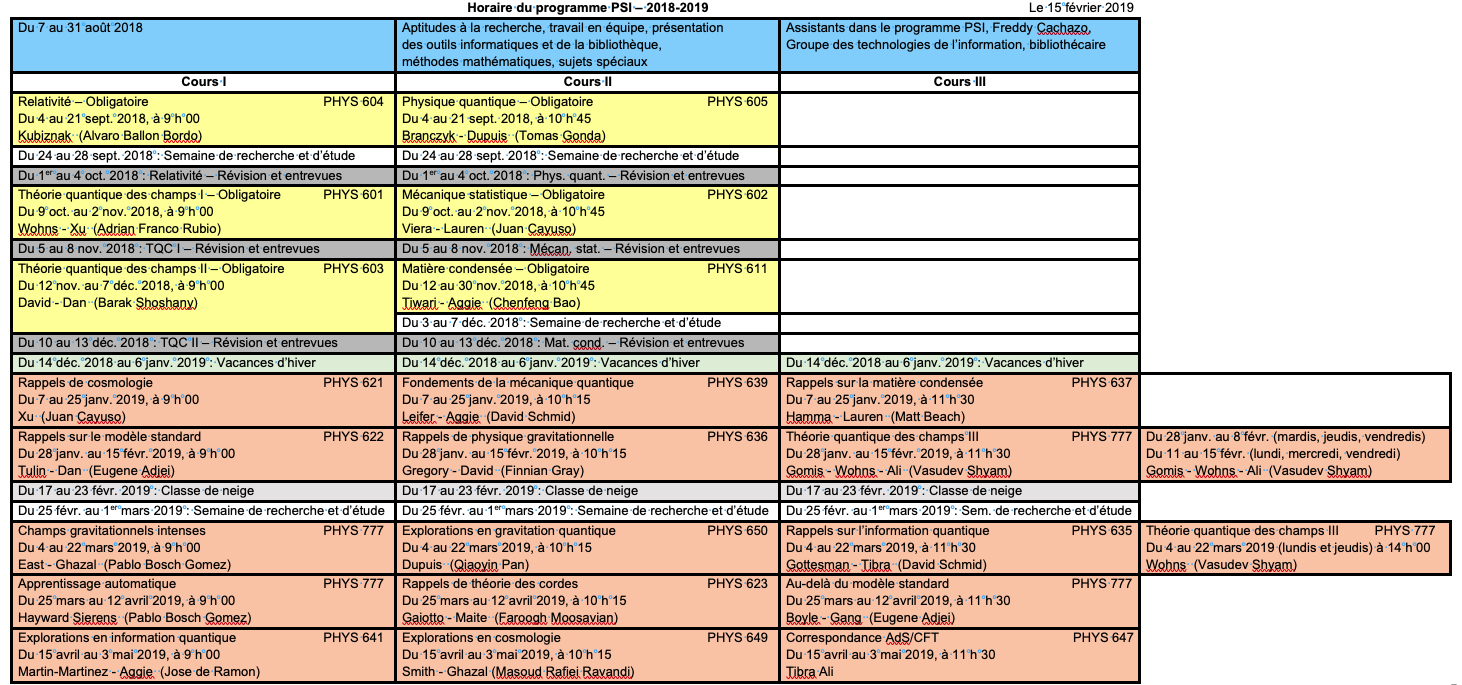
Le programme comprend aussi des cours de mise à niveau en anglais, une formation à la communication scientifique et des ateliers sur la présentation d’exposés. Voici à titre d’exemple l’horaire de l’année 2022-2023. L’horaire peut être modifié d’une année à l’autre, en fonction des besoins des étudiants.
Évaluation
Même si tous les cours donnent lieu à une note de « Réussite » ou « Échec », la méthode préconisée dans le programme PSI est celle d’une évaluation continue effectuée par le personnel enseignant. Cette évaluation prend la forme d’entrevues orales (pour les cours obligatoires), de devoirs et de contribution aux séances de travaux dirigés. Le but visé est d’encourager tous les étudiants à atteindre leur plein potentiel et d’éviter la compétition pour les notes.
Cours du programme PSI
Ces cours ont lieu de septembre à janvier. D’une durée de 5 semaines chacun, ils couvrent des sujets fondamentaux au niveau des études supérieures. Les étudiants doivent suivre 7 des 8 cours obligatoires. Vous trouverez ci-après une description de versions récentes des cours obligatoires. Noter que les cours et les sujets couverts peuvent changer et que les descriptions ci-dessous peuvent ne pas correspondre au contenu de l’année qui vient.
Physique classique
Ce cours vise à revoir les bases de la mécanique classique, de la relativité restreinte et de la théorie classique des champs, en insistant sur les notions de géométrie et sur le formalisme relativiste.
Physique quantique
Ce cours sur la mécanique quantique comporte 2 parties.
La première partie vise à revoir les fondements de la mécanique quantique et à donner un aperçu de la théorie des perturbations afin de traiter des perturbations dans des systèmes quantiques. On aborde l’évolution dans le temps des systèmes quantiques à l’aide des équations de Schrödinger et de Heisenberg, ainsi que des schémas d’interaction. On aborde aussi les fondements de la mécanique statistique quantique pour les particules reconnaissables, les bosons et les fermions. On donne un bref aperçu de la méthode des matrices de densité et de l’interaction de systèmes quantiques avec leur environnement.
La 2e partie du cours consiste en une introduction à la théorie des champs quantiques scalaires. On présente la technique des diagrammes de Feynman pour la théorie des perturbations et on l’applique à la diffusion de particules relativistes. On aborde brièvement la renormalisation.
Théorie quantique des champs I
Le cours commence par la recherche d’une théorie quantique qui soit compatible avec la relativité restreinte, sans supposer que les champs soient fondamentaux. Néanmoins, les champs s’avèrent un outil mathématique très bon, peut-être même indispensable, pour formuler et étudier une telle théorique quantique relativiste. La seconde partie du cours présente la théorie de Dirac et sa quantification canonique, ainsi que la quantification de la théorie des champs de Maxwell. On y développe la technique des diagrammes de Feynman pour la théorie des perturbations et on l’applique à la diffusion de fermions et photons relativistes. On présente la renormalisation de l’électrodynamique quantique à l’ordre d’une boucle.
Relativité
Il s’agit d’un cours d’introduction à la relativité générale (RG). On aborde les bases de la géométrie différentielle et ses applications à la théorie de la gravitation d’Einstein. Le but visé est d’aborder les trous noirs, les ondes gravitationnelles et les preuves observationnelles de la RG, ainsi que certains sujets plus avancés.
Théorie quantique des champs II
Ce cours comporte 3 parties. La 1re partie porte sur la formulation d’intégrales de chemin en mécanique quantique non relativiste et la formulation d’intégrales fonctionnelles en théorie quantique des champs. La 2e partie aborde la renormalisation et le groupe de renormalisation. La 3e partie porte sur la quantification de théories de jauge non abélienne à l’aide de techniques d’intégrales fonctionnelles.
Physique statistique
Ce cours aborde dans une première partie plusieurs sujets de physique statistique à l’état d’équilibre, notamment les transitions d’état et le groupe de renormalisation. La 2e partie du cours porte sur la physique statistique dans des états de non-équilibre, notamment la cinétique de l’agrégation, la dynamique des spins, la dynamique des populations et les réseaux complexes.
Ces cours ont lieu de janvier à avril. Les cours au choix initient les étudiants à des sujets de l’heure et à des sujets de recherche de pointe dans divers sous-domaines spécialisés. Les étudiants doivent suivre au moins 6 cours. Le nombre total de cours au choix change chaque année et se situe généralement entre 12 et 15. Chaque cours dure 5 semaines. Vous trouverez ci-après une description de versions récentes des cours au choix. Noter que les cours et les sujets couverts peuvent changer et que les descriptions ci-dessous peuvent ne pas correspondre au contenu de l’année qui vient.
Voici quelques cours et sujets récents.
Matière condensée
Rupture spontanée de symétries continues. Modes de Goldstone. Modèle sigma non linéaire. Expansion 2+epsilon et 1/N. Fusion 2d. État hexatique. Chaînes de spins quantiques. Bosonisation. Liquide de Luttinger. Liquide de Fermi. Instabilité de Cooper. Groupe de renormalisation de Shankar-Polchinski. Supraconductivité selon la théorie BCS.
Fondements quantiques
Problème de l’interprétation standard de la mécanique quantique. Opérationalisme et réalisme. Problème de la mesure quantique et classification des programmes de recherche selon la solution qu’ils proposent. Formulation de la physique quantique en tant que théorie opérationnelle : opérateurs de densité; mesures établies à l’aide d’un opérateur positif; correspondances complètement positives préservant la trace; purification; extension de Naimark; dilatation de Stinespring. Axiomatisations opérationnelles de la physique quantique. Modèles à variable cachée et distinction entre modèle psi-ontique et modèle psi-épistémique. Modèles à variable cachée fondés sur une restriction épistémique. Théorème de Bell et localité. Théorème de Kochen-Specker et non-contextualité. Interprétation de de Broglie-Bohm. Théories d’effondrement dynamique. Interprétation d’Everett.
Physique gravitationnelle
Ce cours vise principalement à aborder certains sujets avancés de physique gravitationnelle et de ses applications à la physique des hautes énergies. Les outils mathématiques requis seront présentés au fur et à mesure des besoins.
Information quantique
Formulation de la physique quantique en tant que théorie opérationnelle. Calcul réversible. Portes quantiques. Complexité. Algorithmes. Correction d’erreurs. Cryptographie et théorie de l’information.
Cosmologie
Univers de Friedmann-Lemaître-Robertson-Walker. Énergie sombre. Rayonnement fossile. Nucléosynthèse primordiale. Matière sombre. Cosmologie lambda CDM. Inflation cosmique. Perturbations primordiales. Théorie quantique des champs dans un espace-temps courbe.
Apprentissage automatique pour la physique des systèmes à N corps
Ce cours vise à présenter des techniques d’apprentissage automatique pour l’étude de problèmes de systèmes à N corps classiques et quantiques concernant la matière quantique, l’information quantique et des domaines connexes de la physique. Les exposés mettent l’accent sur les liens entre la physique statistique et l’apprentissage automatique. Les séances de travaux dirigés et les devoirs sont centrés sur l’acquisition de compétences de programmation en langage Python pour l’apprentissage automatique. Les sujets abordés comprennent les techniques d’apprentissage supervisé, les réseaux neuronaux à propagation avant, les réseaux neuronaux convolutifs, l’apprentissage non supervisé pour la visualisation et le groupement de données par classe, de même que les recherches de pointe à la jonction de la physique et de l’apprentissage automatique.
Théorie quantique des champs et théorie des cordes
Théorie conforme des champs. Anomalies. Introduction à la théorie des cordes.
Information quantique relativiste (IQR)
Qu’est-ce que l’IQR? Sujets de recherche en IQR. Mesure de champs quantiques; le problème de la mesure et la relativité. Qu’est-ce qu’un détecteur de particules? L’interaction entre lumière et matière à partir des principes premiers. Détecteurs d’Unruh-DeWitt; information quantique pratique sur des théories quantiques des champs (TQC). Relativité, covariance et optique quantique; un regard critique sur l’approximation unimodale et l’approximation de l’onde tournante. Mesure de fluctuations du vide. Détecteurs non inertiels de particules et qubits dans des espaces-temps courbes. L’effet Unruh : dérivation originale avec une perspective d’information quantique. Thermalité. Conditions de Gibbs et de Kubo-Martin-Schwinger (KMS). Quand la condition de Gibbs ne suffit pas : la condition de KMS en TQC. Thermalisation de détecteurs de particules accélérées : l’effet Unruh; dérivation moderne. Structure d’intrication d’une TQC. Introduction à la récupération d’intrication dans le vide. Téléportation quantique d’énergie et violation des conditions sur l’énergie.
Théorie de Chern-Simons
Rappels sur les formes différentielles et très bref aperçu de la cohomologie. Rappels sur les champs de jauge, l’invariance de jauge, l’intensité de champ et les lignes de Wilson. Le lagrangien de Chern-Simons. Invariance de jauge et quantification du niveau. Les lignes de Wilson et leur invariance topologique. Invariants de nœuds des lignes de Wilson. Polynôme de Jones, et relation entre lignes de Wilson et polynôme de Jones. L’espace des phases et l’espace de Hilbert sur une surface riemannienne. Actions sur le groupe de tresses de l’espace de Hilbert en présence de lignes de Wilson, et équation de Knizhnik-Zamolodchikov.
Gravitation quantique
Formulation canonique de systèmes contraints. Programme de Dirac. Formalisme de premier ordre de la gravitation. Gravitation quantique à boucles. Modèles de mousse de spin. Discussions avec des orateurs invités sur : l’espace et le temps en gravitation quantique; la cosmologie quantique à boucles; les trous noirs; d’autres approches de la gravitation quantique; les méthodes numériques dans les modèles de mousse de spin; les recherches menées à l’Institut Périmètre.
Modèle standard
Particules et lagrangien du modèle standard avec application de la théorie de Yang et Mills. Théorie effective du modèle standard à rupture spontanée de symétrie. Neutrino droitier. Application à la physique des particules : règles de Feynman pour le modèle standard.
Le programme PSI bénéficie du soutien des personnes et organismes suivants : la Fondation familiale Savvas-Chamberlain; la Fondation du patrimoine hellénique; la famille Marsland; des membres du Cercle Emmy-Noether.