|
Precomputes the coefficients needed to evolve a state using ChebyshevStep(), for time timestep, with accuracy prec.
ChebyshevPrep() constructs the coefficients of a polynomial in a Hamiltonian 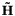 that approximates that approximates 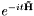 (where (where 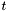 is given by is given by timestep) with an error of no more than prec (provided that 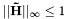 . These coefficients are returned in the vector PowerCoeffs. . These coefficients are returned in the vector PowerCoeffs.
The order of approximation required (N) depends on both timestep and prec. We first compute an upper bound 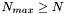 , then generate the coefficients , then generate the coefficients 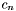 of the of the 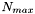 th order approximation, and determine the th order approximation, and determine the 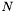 such that such that 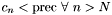 . We then terminate the expansion at . We then terminate the expansion at 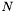 th order, generate the matrix of Chebyshev polynomial coefficients, and transform the series sum of Chebyshev polynomials into a sum of monomials th order, generate the matrix of Chebyshev polynomial coefficients, and transform the series sum of Chebyshev polynomials into a sum of monomials 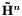 . .
Because the coefficient sequence (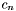 ) is not necessarily decreasing in absolute value, we also compute a bounding sequence ( ) is not necessarily decreasing in absolute value, we also compute a bounding sequence (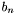 , or , or CoeffsBoundSeq). The bounding sequence is defined so that 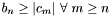 . .
The bounding sequence allows the routine that actually applies 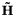 repeatedly to a state (ChebyshevStep()) to do dynamic error estimation. Since repeatedly to a state (ChebyshevStep()) to do dynamic error estimation. Since 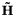 will typically be very contracting (all eigenvalues will be closer to zero than to -1 or 1), the norm of will typically be very contracting (all eigenvalues will be closer to zero than to -1 or 1), the norm of 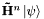 will decrease rapidly with will decrease rapidly with 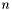 . When it decreases enough (relative to the bounding sequence of the coefficients), ChebyshevStep() can terminate the expansion. . When it decreases enough (relative to the bounding sequence of the coefficients), ChebyshevStep() can terminate the expansion. |
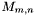 is the coefficient of
is the coefficient of 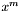 in the
in the 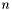 'th Chebyshev polynomial.
'th Chebyshev polynomial. 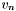 is the coefficient of the
is the coefficient of the 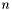 'th Chebyshev polynomial in the expansion of
'th Chebyshev polynomial in the expansion of 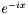 .
. 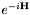 , placing the result in
, placing the result in 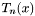 is represented by the
is represented by the  th row is the coefficient of
th row is the coefficient of  as a weighted sum of Chebyshev polynomials (i.e., a Chebyshev approximation to some other function) into a column vector that represents the same function as a polynomial in
as a weighted sum of Chebyshev polynomials (i.e., a Chebyshev approximation to some other function) into a column vector that represents the same function as a polynomial in 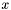 .
. time) using the recursion relation
time) using the recursion relation 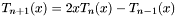 , with
, with 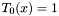 and
and 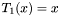 .
. 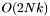 time, as compared to
time, as compared to 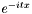 in Chebyshev polynomials. The expansion is computed by
in Chebyshev polynomials. The expansion is computed by 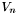 . The coefficients can be worked out analytically, and turn out to be Bessel
. The coefficients can be worked out analytically, and turn out to be Bessel 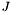 functions:
functions: ![\[ V_n = (2i)^n J_n(t) \]](form_39.png)
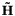 that approximates
that approximates 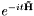 (where
(where 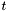 is given by
is given by 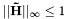 . These coefficients are returned in the vector PowerCoeffs.
. These coefficients are returned in the vector PowerCoeffs.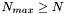 , then generate the coefficients
, then generate the coefficients 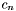 of the
of the 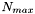 th order approximation, and determine the
th order approximation, and determine the 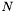 such that
such that 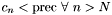 . We then terminate the expansion at
. We then terminate the expansion at 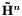 .
.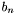 , or
, or 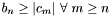 .
.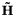 repeatedly to a state (
repeatedly to a state (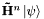 will decrease rapidly with
will decrease rapidly with  1.4.4
1.4.4