
#include "linalg.h"
#include "quantum.h"
#include <gsl/gsl_sf_bessel.h>
#include <gsl/gsl_errno.h>
Include dependency graph for Chebyshev.cpp:

Functions | |
| void | GenerateChebyshevMatrix (itype N, DenseMatrix< complex > &M) |
Computes an NxN matrix, where 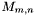 is the coefficient of is the coefficient of 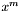 in the in the 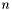 'th Chebyshev polynomial. 'th Chebyshev polynomial. | |
| void | ResizeChebyshevMatrix (itype N, DenseMatrix< complex > &M) |
| Efficiently resizes an existing Chebyshev polynomial matrix to NxN, using the coefficients already computed. | |
| void | GenerateChebyshevEvolutionVector (double time, itype N, DenseVector< complex > &V) |
Computes an N-element vector, where 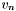 is the coefficient of the is the coefficient of the 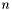 'th Chebyshev polynomial in the expansion of 'th Chebyshev polynomial in the expansion of 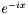 . . | |
| int | ChebyshevPrep (double timestep, double prec, DenseVector< complex > &PowerCoeffs, DenseVector< double > &CoeffsBoundSeq) |
Precomputes the coefficients needed to evolve a state using ChebyshevStep(), for time timestep, with accuracy prec. | |
A standard and nontrivial task in quantum simulations is to compute the unitary evolution of a state vector:
![\[ \left|\psi\right\rangle \longrightarrow \left|\psi(t)\right\rangle = e^{-i\mathbf{H}t}\left|\psi\right\rangle \]](form_0.png)
Matrix exponentiation is nontrivial, especially if the matrix in question is very large. However, computing 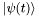 does not actually require computing
does not actually require computing 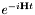 , or even
, or even 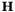 . It can be written as a power series in
. It can be written as a power series in 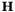 :
:
![\[ e^{-i\mathbf{H}t}\left|\psi\right\rangle \approx \left(\mathbf{1} -i\mathbf{H}t - \frac{t^2}{2}\mathbf{H}^2\ldots\right) \left|\psi\right\rangle \]](form_4.png)
This requires only that we compute 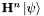 , which in turn can be done recursively if we can compute
, which in turn can be done recursively if we can compute 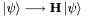 .
.
The Taylor expansion given above turns out to converge rather slowly; the Taylor series is optimized for local convergence at 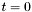 , at the cost of all larger
, at the cost of all larger 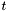 . Other power series expansions exist, and have better global convergence properties. The power series with the best global convergence properties over a fixed intervals is the Chebyshev series:
. Other power series expansions exist, and have better global convergence properties. The power series with the best global convergence properties over a fixed intervals is the Chebyshev series:
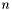 th Chebyshev polynomial
th Chebyshev polynomial 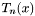 is an
is an 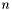 th order polynomial in
th order polynomial in 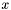 , defined on
, defined on ![$ x \in [-1\ldots 1] $](form_12.png) .
.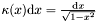 , so letting
, so letting 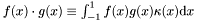 , we have
, we have 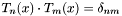 .
.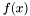 can be expanded as
can be expanded as
![\[ f(x) \approx \tilde{f}_N(x) = \sum_{n=0}^N{\left[f(x) \cdot T_n(x)\right] T_n(x)} \]](form_17.png)
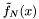 is almost as close to
is almost as close to 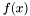 , by
, by 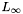 distance (on the interval
distance (on the interval ![$ x \in [-1\ldots 1] $](form_12.png) !) as the optimal
!) as the optimal 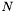 'th order polynomial approximation.
'th order polynomial approximation.
This makes Chebyshev polynomials ideally suited for quantum state evolution. When they are generalized to matrices, the argument 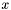 becomes a matrix, which typically has many eigenvalues. We want the approximation of
becomes a matrix, which typically has many eigenvalues. We want the approximation of 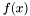 to be accurate for all the eigenvalues. This motivates the uniform convergence of the Chebyshev polynomial expansion. It is necessary to bound the highest and lowest eigenvalues of
to be accurate for all the eigenvalues. This motivates the uniform convergence of the Chebyshev polynomial expansion. It is necessary to bound the highest and lowest eigenvalues of 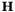 , and then rescale energy and time so that
, and then rescale energy and time so that 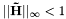 , but once this is done, computing the correct power series is straightforward. From the rescaled time
, but once this is done, computing the correct power series is straightforward. From the rescaled time 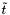 , it is possible to identify how many coefficients will be needed to approximate the matrix exponential well; beyond a critical value, the error declines exponentially.
, it is possible to identify how many coefficients will be needed to approximate the matrix exponential well; beyond a critical value, the error declines exponentially.
Representing 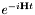 as a power series in
as a power series in 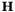 requires first computing the Chebyshev polynomials themselves. The method GenerateChebyshevMatrix() does this via a simple recursion relation, storing the coefficient of
requires first computing the Chebyshev polynomials themselves. The method GenerateChebyshevMatrix() does this via a simple recursion relation, storing the coefficient of 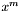 in
in 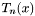 as an element
as an element 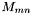 in a (triangular) matrix. If more coefficients are needed later, ResizeChebyshevMatrix() can compute just the additional ones needed.
in a (triangular) matrix. If more coefficients are needed later, ResizeChebyshevMatrix() can compute just the additional ones needed.
The second step involves computing the expansion of 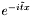 in Chebyshev polynomials. The method GenerateChebyshevEvolutionVector() does this using Bessel functions (borrowed from the Gnu Scientific Library), and stores the expansion in a complex vector. The coefficients of
in Chebyshev polynomials. The method GenerateChebyshevEvolutionVector() does this using Bessel functions (borrowed from the Gnu Scientific Library), and stores the expansion in a complex vector. The coefficients of 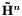 in the approximated matrix exponential can then be computed by matrix-vector multiplication.
in the approximated matrix exponential can then be computed by matrix-vector multiplication.
For a particular Hamiltonian and time, ChebyshevPrep() first determines what order approximation will be required to bound the error by some very small number, then computes the coefficients. A single step of duration 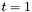 can then be accomplished by ChebyshevStep(). The entire process of evolving for time
can then be accomplished by ChebyshevStep(). The entire process of evolving for time 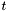 (including both ChebyshevPrep() and ChebyshevStep()), can be done in one step using ChebyshevEvolve().
(including both ChebyshevPrep() and ChebyshevStep()), can be done in one step using ChebyshevEvolve().
However, taking a single step of large duration can lead to substantially increased error -- not because of error in the Chebyshev polynomials, but because the coefficients become so large for high-order approximations that they amplify rounding errors. This could very likely be taken care of by a more sophisticated method of evaluating polynomials, but this would require keeping additional temporary vectors (e.g., 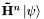 for several values of
for several values of 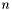 ), which could be memory-intensive for extremely large vectors. As an alternative, ChebyshevStepEvolve() will automatically break up large timesteps into several smaller jumps of bounded size.
), which could be memory-intensive for extremely large vectors. As an alternative, ChebyshevStepEvolve() will automatically break up large timesteps into several smaller jumps of bounded size.
While the Chebyshev polynomial method is (unlike split-operator or Cayley methods) not explicitly norm-preserving, its accuracy is so absurdly good (errors are typically 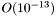 in double precision) that unitarity is not a concern.
in double precision) that unitarity is not a concern.
 1.4.4
1.4.4