|
Functions |
|
State | QubitSpinState (double x, double y, double z) |
| | Returns a J=1/2 pure state so that <X>=x, <Y>=y, and <Z>=z, up to normalization.
|
|
State | ZPlus () |
| | Returns the +1 eigenstate of SigmaZ.
|
|
State | ZMinus () |
| | Returns the -1 eigenstate of SigmaZ.
|
|
State | XPlus () |
| | Returns the +1 eigenstate of SigmaX.
|
|
State | XMinus () |
| | Returns the -1 eigenstate of SigmaX.
|
|
State | YPlus () |
| | Returns the +1 eigenstate of SigmaY.
|
|
State | YMinus () |
| | Returns the -1 eigenstate of SigmaY.
|
|
State | QubitMUBState (itype i) |
| | Returns the ith state from the 6-element qubit MUB set: {|0>, |1>, |+>, |->, |+i>, |-i>}.
|
|
State | QubitSICPState (itype i) |
| | Returns the ith state from a 4-element qubit SICPOVM chosen so that the 1st is |0>, and the 2nd is in the X-Z plane.
|
|
Operator | Identity (itype D) |
| | Returns the identity operator in D dimensions.
|
|
Operator | Zero (itype D) |
| | Returns the zero operator in D dimensions.
|
|
Operator | QubitSpinOperator (double x, double y, double z) |
| | Returns an arbitrary J=1/2 spin operator 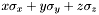 . .
|
|
Operator | Hadamard () |
| | Returns the Hadamard matrix for qubits.
|
|
Operator | HalfPhase () |
| | Returns the phase-flip matrix (square root of SigmaZ) for qubits.
|
|
Operator | SigmaI () |
| | Returns the J=1/2 Identity operator.
|
|
Operator | SigmaX () |
| | Returns the J=1/2 Pauli spin operator along the X axis.
|
|
Operator | SigmaY () |
| | Returns the J=1/2 Pauli spin operator along the Y axis.
|
|
Operator | SigmaZ () |
| | Returns the J=1/2 Pauli spin operator along the Z axis.
|
|
Operator | Sigma (itype i) |
| | Returns the ith matrix from the Pauli group, {X,Y,Z,I}.
|
|
Operator | Jz (itype d) |
| | Returns the Jz (angular momentum along the z-axis) operator in d dimensions.
|
|
Operator | Jx (itype d) |
| | Returns the Jz (angular momentum along the z-axis) operator in d dimensions.
|
|
Operator | Jy (itype d) |
| | Returns the Jz (angular momentum along the z-axis) operator in d dimensions.
|
|
Operator | Jn (itype d, double x, double y, double z) |
| | Returns the d-dimensional angular-momentum-along-the-(x,y,z)-axis operator.
|
The ConstStates namespace contains pre-defined states and operators that are frequently used in quantum information processing. These include:
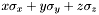 .
.  1.4.4
1.4.4