
|
Collaboration diagram for Functions and operations:

|
Functions | |
| template<class T> | |
| DenseMatrix< T > | Commutator (const DenseMatrix< T > &m1, const DenseMatrix< T > &m2) |
Creates a new DenseMatrix containing the commutator of two DenseMatrices: ![$[A,B] = AB-BA$](form_64.png) . . | |
| template<class T> | |
| DenseMatrix< T > | AntiCommutator (const DenseMatrix< T > &m1, const DenseMatrix< T > &m2) |
Creates a new DenseMatrix containing the anticommutator of two DenseMatrices: 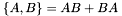 . . | |
| template<class T> | |
| DenseMatrix< T > & | scavenge (DenseMatrix< T > &m, typename linalg_traits< T >::abs_type minabs) |
Sets all the entries of m whose absolute value falls below minabs to zero, and returns a reference to the result. | |
| template<class T> | |
| DenseVector< T > & | scavenge (DenseVector< T > &v, typename linalg_traits< T >::abs_type minabs) |
Sets all the entries of v whose absolute value falls below minabs to zero, and returns a reference to the result. | |
| template<class T> | |
| DenseMatrix< T > | scavenge (const DenseMatrix< T > &m, typename linalg_traits< T >::abs_type minabs) |
Creates a new DenseMatrix which is a scavenged copy of m, and returns it. | |
| template<class T> | |
| DenseVector< T > | scavenge (const DenseVector< T > &v, typename linalg_traits< T >::abs_type minabs) |
Creates a new DenseVector which is a scavenged copy of m, and returns it. | |
| double | Entropy (Operator &rho) |
Computes the Von Neumann entropy 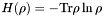 of the positive semidefinite matrix of the positive semidefinite matrix rho. | |
| double | LinearEntropy (Operator &rho) |
Computes the linear entropy 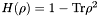 of the positive semidefinite matrix of the positive semidefinite matrix rho. | |
| Operator & | RandomMixedState (Operator &Rho, itype Nancillae) |
| Assigns to Rho a random mixed state from the induced measure on 1+Nancillae copies. | |
| Operator & | HaarRandomize (Operator &Rho) |
Assigns to Rho a random pure state. Equivalent to RandomMixedState() with Nancillae=0. | |
| Operator & | HilbertSchmidtRandomize (Operator &Rho) |
Assigns to Rho a positive semidefinite matrix selected from Hilbert-Schmidt measure. Equivalent to RandomMixedState() with Nancillae=1. | |
| double | TraceNorm (Operator &M) |
| Computes the sum of the absolute values of the eigenvalues of a Hermitian matrix M. | |
| double | InfinityNorm (Operator &M) |
Computes the square root of the largest eigenvalue of 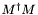 . If . If 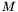 is Hermitian, then this is the maximum of the absolute values of is Hermitian, then this is the maximum of the absolute values of 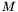 's eigenvalues. 's eigenvalues. | |
| double | Fidelity (Operator &Sigma, Operator &Rho) |
Computes the fidelity between two states as ![$ F = \left[\mathrm{Tr}\sqrt{\sqrt{\rho}\sigma\sqrt{\rho}}\right]^2 $](form_73.png) . . | |
| double | Fidelity (Operator &Sigma, State &Psi) |
Computes the fidelity between a mixed state 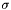 and a pure state and a pure state 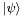 : : 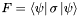 . . | |
| double | Fidelity (State &Psi, Operator &Rho) |
Computes the fidelity between a pure state 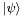 and a mixed state a mixed state and a mixed state a mixed state 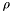 : : 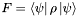 . . | |
| double | Fidelity (State &Psi, State &Phi) |
Computes the fidelity between two pure states 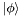 and and 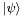 : : 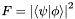 . . | |
| double | NullspaceProjection (Operator &Sigma, Operator &Rho, double MinProbability=DBL_EPSILON) |
Computes the projection of 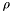 onto the nullspace of onto the nullspace of 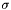 . . | |
| double | RelativeEntropy (Operator &Sigma, Operator &Rho, double MinProbability=DBL_EPSILON) |
Computes the relative entropy, or Kullback-Leibler divergence, of 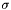 relative to relative to 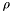 : : 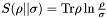 . . | |
| void | RelativeEntropyAndNullProjection (double &RelEnt, double &NullProj, Operator &Sigma, Operator &Rho, double MinProbability) |
Computes the relative entropy of 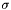 relative to relative to 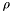 and the projection of and the projection of 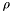 onto onto 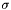 's null space. 's null space. | |
| Operator & | Positivize (Operator &M) |
| Converts M to a positive-definite matrix by replacing all its negative eigenvalues with 0. | |
| Operator & | SquareRoot (Operator &M) |
| Replaces the Hermitian positive-definite matrix M with its unique positive-definite square root. | |
| template<class Op> | |
| double | Entanglement (const State &psi, const TensorProductStructure &Universe, ISet &SubSystem, Op EntropyFunction) |
Computes the bipartite entanglement of psi between SubSystem and its complement, using the user-supplied EntropyFunction. | |
| double | Entanglement (const State &psi, const TensorProductStructure &Universe, ISet &Subsystem) |
Computes the bipartite entanglement of psi between SubSystem and its complement, using Von Neumann entropy. | |
|
||||||||||||||||
|
Sets all the entries of
For complex-valued matrices, |
|
||||||||||||||||
|
Sets all the entries of
For complex-valued vectors, |
|
|
Computes the Von Neumann entropy
The Von Neumann entropy is computed by diagonalizing the density matrix, and computing the sum of
|
|
||||||||||||
|
Assigns to Rho a random mixed state from the induced measure on 1+Nancillae copies.
There is no unique measure from which to choose a random mixed state. One appealing class of measures is the set of induced measures obtained by partial-tracing a random pure state (according to Haar measure) on a larger system. This function generates such a state for a Warning: be cautious in setting Nancillae too high; generating the state could take huge amounts of memory, increasing exponentially with Nancillae. |
|
||||||||||||
|
Computes the fidelity between two states as Both arguments must be positive-definite, or the routine will complain to std::cerr and return 0. This routine is rather computationally intensive, so if one of the two states is known to be pure, use the faster routine for that case. |
|
||||||||||||||||
|
Computes the projection of
This can be interpreted as the maximum of the probability that an event for which |
|
||||||||||||||||
|
Computes the relative entropy, or Kullback-Leibler divergence, of
If |
|
||||||||||||||||||||||||
|
Computes the relative entropy of
The results are stored in RelEnt and NullProj, respectively. The parameter MinProbability divides the eigenvalues of
|
|
|
Replaces the Hermitian positive-definite matrix M with its unique positive-definite square root.
NOTE: if the argument turns out not to be positive-definite, then the result is non-unique, non-Hermitian, and will be constructed by setting |
|
||||||||||||||||||||||||
|
Computes the bipartite entanglement of
The entropy function should be a function pointer or class such that for a density matrix |
 1.4.4
1.4.4