Public Member Functions
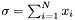 .
. 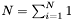 .
. 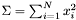 .
. 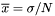 .
. 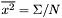 .
. 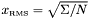 .
. 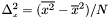 .
. 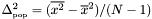 .
. 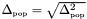 .
. 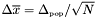 .
. num to the accumulator. -num to the accumulator. NOTE: does not delete a sample!
#include <quantum.h>
Public Member Functions | |
| Accumulator () | |
| Default constructor: creates an empty accumulator. | |
| number | Sum () |
Returns the sum of all accumulated samples. 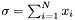 . . | |
| number | Count () |
Returns the number of samples accumulated. 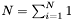 . . | |
| number | SqSum () |
Returns the sum of the squares of all accumulated samples: 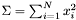 . . | |
| number | Mean () |
Returns the sample mean: 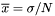 . . | |
| number | MeanSq () |
Returns the mean of the squares: 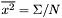 . . | |
| number | RMS () |
Returns the RMS value: 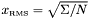 . . | |
| number | SampleVariance () |
Returns the sample variance: 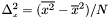 . . | |
| number | PopVariance () |
Returns the estimated population variance: 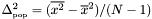 . . | |
| number | PopStdDev () |
Returns the estimated standard deviation of the population: 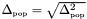 . . | |
| number | StdDevMean () |
Returns the estimated standard deviation of the mean: 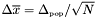 . . | |
| Accumulator & | Reset () |
| Discards all samples. | |
| Accumulator & | operator+= (number num) |
Adds a sample num to the accumulator. | |
| Accumulator & | operator-= (number num) |
Adds a sample -num to the accumulator. NOTE: does not delete a sample! | |
The Accumulator class is a convenient way to compute certain statistics for a stream of (currently) real numbers. Extending this to other types would be fairly easy. Statistics that can be computed are:
 1.4.4
1.4.4