The Ultra-Strong Equivalence Principle
and the ``IR completion” of gravity.
Much of the efforts of theoretical physicists is devoted to the fascinating problem of finding a consistent Ultra Violet-completion for Gravity (see Perimeter’s string theory and quantum gravity groups). However, there are good chances that whatever happens at the highest energies effectively ``decouples”, so that (i) all that we can possibly experiment in the next few lives is oblivious to the UV details and can always be encoded at the low-energy effective level; (ii) if difficulties appear at low energy, those are not going to be solved by changing the UV structure of the theory. In fact, the well established effective paradigm for gravity,
(*)
is not free of difficulties, already at low energy! For instance:
3) ...Cosmology! (yes, we can fit our observations very well but at what price? We need to assume two epochs of accelerated expansion (inflation and dark energy), characterized by widely separated mass scales, that require appropriate negative pressure components and tremendous fine tunings).
In the recent years I have been fascinated by the idea of a substantial reassessment of the present description of gravity in the low-energy regime that could possibly address those problems. So I worked on it. For technical details see the bibliography at the end of this page and especially this. For some more informal free-wheeling thoughts keep reading:
A) Forget about the UV for a second, the above mentioned difficulties have probably to do with the IR-side of the picture.
B) Perhaps, IR modifications of GR have not been daring enough so far. GR assumes (i) that spacetime is described by a metric manifold and (ii) the dynamics of the metric field on that manifold is given by the Einstein Hilbert action. So far, only point (ii) has been questioned and modified. Try with point (i).
C) Copy GR: do to GR what GR did to flat space. Modify the geometric description of GR at large distances in the same way in which - at large distances - a curved manifold modifies flat space.
D) By changing the geometric description at large distances you can still do local physics: In the small distance limit recover the metric manifold and the usual local theory GR + matter fields (*)
E) No need of a new mass scale. Copy GR again. The breakdown of flat space, non-gravitational physics, in GR, happens at distances of order the curvature radius. Apply the same to GR. Modify its geometrical description by subleading curvature-dependent contributions.
F) Relation to Dark Energy: supernovae observations are affected by point E) because high redshit objects (at any time) are placed from the observer at a distance of order the inverse curvature. The only coincidence is that of looking as far away as the Hubble scale. No need of a new mass scale!
G) Any guiding principles for the deformation? Take GR’s Equivalence Principle and make it Ultra-Strong!

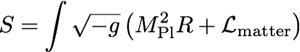
Bibliography:
F. Piazza, ``Modifying Gravity in the Infra-Red by imposing an 'Ultra-Strong' Equivalence Principle''
To appear in the December 2009 Special Issue of Int. J. Mod. Phys. D, 0907.4299
(Honorable mention at the Gravity Research Foundation Essay Competition 2009)
F. Piazza, ``The IR-Completion of Gravity: What happens at Hubble Scales?'', New J. Phys. 11 (2009) 113050 0907.0765
S. Nesseris, F. Piazza and S. Tsujikawa, ``The universe is accelerating. Do we need a new mass scale?'' 0910.3949
F. Piazza, ``Some new views on gravity at low energy'' 0910.4677

The Ultra-Strong Equivalence Principle:
For each matter field or sector sufficiently decoupled from all other matter fields, there exists a state, the ``vacuum", for which the expectation value of the (bare) energy momentum tensor reads the same as in flat space, regardless of the configuration of the gravitational field.
H) The terms that have to be killed (the ones that are not there in flat space) are IR with respect to the quartically divergent piece and therefore can be reabsorbed by means of an IR-modification, or ``completion”, of standard semiclassical gravity. Such terms seem also related with two traditional problems of the low-energy paradigm:
I) If, as postulated, the VEV of the bare energy momentum tensor amounts to the same value as in flat space, you don’t need to renormalize it anymore. At least at the level of semiclassical gravity, the cosmological constant problem reduces to a readjustment of the zero-point energy, as in flat space.
J) If, in the IR completed theory, the bare energy momentum tensor is the same as in flat space, then you don’t have particle production nor BH information loss.
Invited Talks:
``The accelerating Universe: new physics at small energy”, APC, Paris, Feb 5, 2009
``Modifying Gravity in the Infra-Red by imposing an Ultra-Strong equivalence principle"
New Prospects for Solving the Cosmological Constant Problem, Perimeter Institute, May 25-27, 2009
``The IR-completion of Gravity: What happens at Hubble scales?"
Emergent Gravity IV, University of British Columbia, Vancouver, August 24-28 2009.


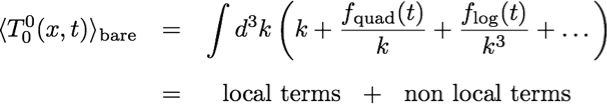


Example: massless scalar on a FRW
