
|
Collaboration diagram for Non-member C-style functions:

|
Modules | |
| Testing Compatibility | |
| Methods that test whether a pair or triple of linear algebraic objects can be combined mathematically. | |
| Copying and assignment | |
| Non-member methods that copy one object into another. | |
| Unary operations | |
| Methods that act on a single object. | |
| Addition and subtraction | |
| Non-member methods that add or subtract one object from another. | |
| Scalar multiplication | |
| Non-member methods that multiply a matrix or vector by a scalar. | |
| Multiplication | |
| Non-member methods that multiply one object by another. | |
| Dot products | |
| External methods that compute the dot product between two objects. | |
| LAPACK routines | |
| Interfaces to sophisticated linear algebraic algorithms from LAPACK. | |
Almost all of the pleasantly object-oriented methods for doing things to linear algebraic objects (primarily operators, either members of classes or global binary operators) call these C-style functions to their dirty work. "C-style" indicates not that they are written in ANSI C (their arguments are templated parameters, and use other C++ functionality, especially pass-by-reference), but that they are fundamentally non-object oriented in design.
Their design is optimized for efficiency rather than for "math-like syntax"; for instance, they return complex structures by computing them directly into a "result" parameter that must be provided, rather than by pushing them onto the stack.
When possible, these routines interface with BLAS (routines that will try to use BLAS are noted in the documentation. However, they provide all the basic linear algebra functionality, such as vector addition or matrix multiplication, independently of BLAS. Each function is overloaded to operate both on abstract types (e.g., Vector<T>, Matrix<T>) and on specific common variants (DenseVector<T>, DenseMatrix<T>). The "result" parameter, however, must always be a Dense object -- abstract types cannot be constructed and cannot necessarily be written to.
The Dense variants will try to use BLAS, but may be unable to do so. Dense objects can be "sliced", i.e. stored in noncontiguous blocks of memory. For example, consider the extraction of a RowVector and a ColumnVector from an 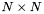 DenseMatrix. It is not possible for both to have their elements stored in consecutive memory locations. Since the LinAlg library respects the FORTRAN convention of storing matrices in column-major order, the ColumnVector will be stored in a contiguous block of
DenseMatrix. It is not possible for both to have their elements stored in consecutive memory locations. Since the LinAlg library respects the FORTRAN convention of storing matrices in column-major order, the ColumnVector will be stored in a contiguous block of 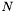 memory locations, while the RowVector will occupy
memory locations, while the RowVector will occupy 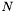 locations spaced at intervals of
locations spaced at intervals of 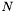 apart. This sort of disjointedness can be handled by the BLAS library; it is known as the "stride" of the object. However, BLAS cannot handle:
apart. This sort of disjointedness can be handled by the BLAS library; it is known as the "stride" of the object. However, BLAS cannot handle:
 1.4.4
1.4.4